Apply and Practice Activity

NSDUH adolescent depression prevalence — Confidence Intervals

Introduction

For this activity you will work with the adolescent data from the National Survey on Drug Use and Health — the same data we worked with in Module 7. The data frame is called NSDUH_adol_depression.Rds.

Here are the variables in the data frame:

Variable	Description
year	Survey year
sex	Biological sex of respondent
age	Age of respondent
raceeth	Race/ethnicity of respondent
mde_past_year	Did the respondent meet criteria for a major depressive episode in the past-year? negative = did not meet criteria, positive = did meet criteria.
mde_lifetime	Did the respondent meet criteria for a major depressive episode in their lifetime? negative = did not meet criteria, positive = did meet criteria.
mh_sawprof	Did the respondent see a mental health care professional in the past-year?
severity_chores	If mde_pastyear is positive, how severely did depression interfere with doing home chores?
severity_work	If mde_pastyear is positive, how severely did depression interfere with school/work?
severity_family	If mde_lifetime is positive, how severely did depression interfere with family relationships?
severity_chores	If mde_pastyear is positive, how severely did depression interfere with social life?
mde_lifetime_severe	If mde_pastyear is positive, was the MDE classified as severe?
substance_disorder	Did the respondent meet criteria for a past-year substance use disorder (alcohol or drug)? — available for 2019 data only
adol_weight	Sampling weight - from sampling protocol
vestr	Stratum — from sampling protocol
verep	Primary sampling unit — from sampling protocol

Recall that in Module 7 we created this graph that depicts the proportion of adolescents with a past-year Major Depressive Episode (MDE) from 2009 to 2019.

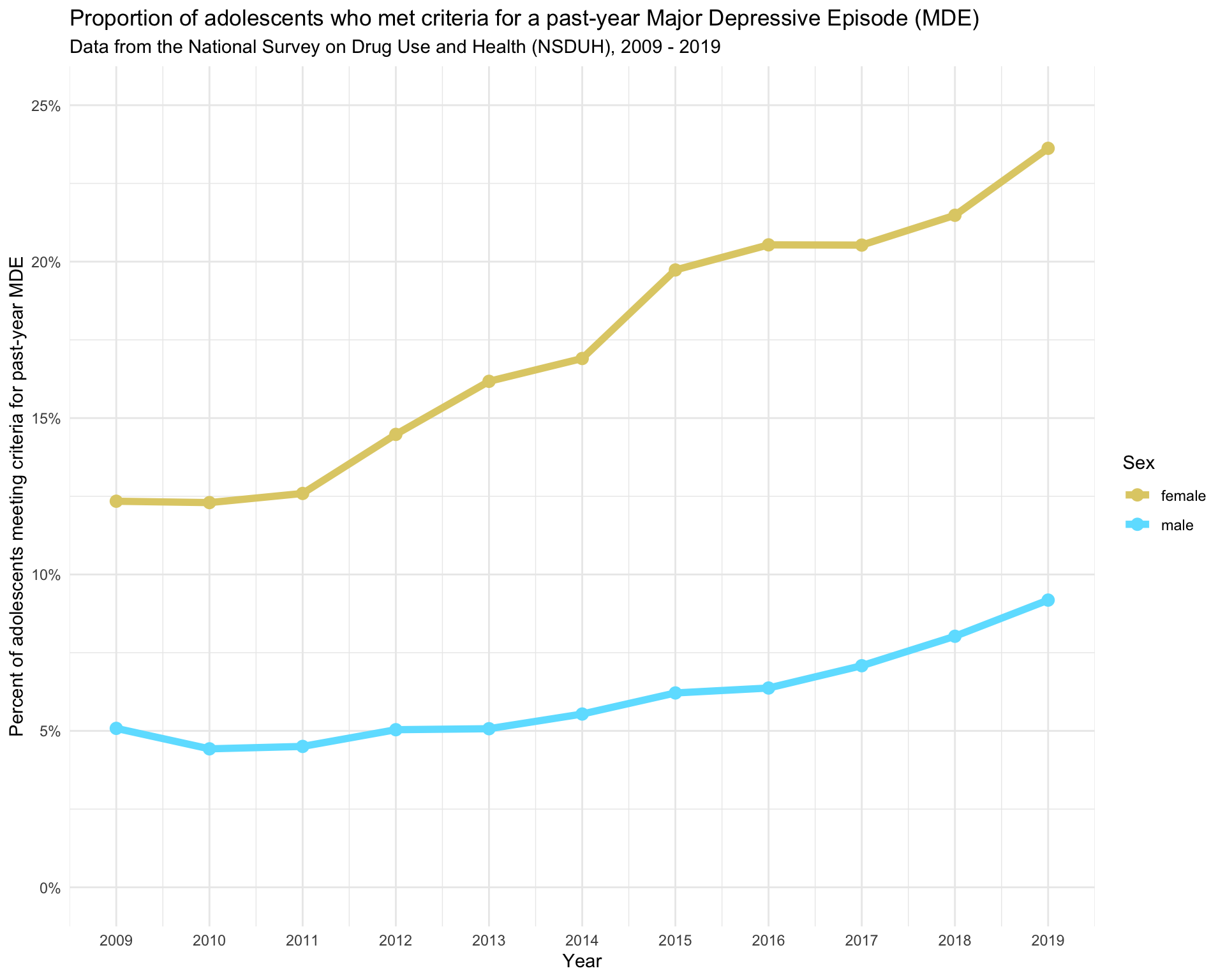
In this Apply and Practice Activity we will update the graph to include Confidence Intervals (CIs) around the point estimates.

Please follow the steps below to complete this activity.

Step by step directions

Step 1

In the Posit Cloud foundations project, navigate to the apply_and_practice folder in the programs folder of the course project. Open up the file called nsduh_confidence_intervals.qmd.

To ensure you are working in a fresh session, close any other open tabs (save them if needed). Click the down arrow beside the Run button toward the top of your screen then click Restart R and Clear Output.

Step 2

First we need to load the packages that are needed for this activity. Find the first level header called

# Load packages

Inside the code chunk load the following packages: gt, gtsummary, survey, here, tidyverse.

Step 3

Find the first level header

# Import data

Inside the code chunk, import the NSDUH data frame (NSDUH_adol_depression.Rds), name it nsduh_20092019.

Step 4

Find the first level header

# Compute a 95% CI (theory-based) for proportion of adolescents with a past-year MDE in 2009

And, the second level header

## Hand calculation of 95% CI

Inside the code chunk write the code needed to calculate the following two quantities:

Number of male and female (separate estimates) respondents who reported their MDE status in 2009.
Proportion of male and female adolescents (separate estimates) with a past-year MDE in 2009.

To do this, create a binary (numeric) version of mde_pastyear, called mde_status, which equals 1 if the individual was positive for a past year MDE, and 0 if the individual was negative for a past year MDE.

From these outputs, calculate a 95% CI using the theory-based/parametric approach for the proportion of male and female adolescents with a past-year MDE (i.e., two separate CIs). Do this by hand, and record your answer in your analysis notebook. Write a few sentences to interpret the CIs.

Step 5

Find the second level header

## Compute the 95% CI using code

Inside the code chunk, write code to calculate the same 95% CI for male and female adolescents.

Verify that you get the same anwswer using your hand calculations and your coded calculations.

We can also ask gtsummary to calculate these proportions for us using the following code.

nsduh_20092019 |> 
  filter(year == 2009 & !is.na(mde_pastyear)) |> 
  select(sex, mde_pastyear) |> 
  tbl_summary(
    by = sex,
    percent = "column",
    label = mde_pastyear ~ "Past-year prevalence of a Major Depressive Episode") |> 
  add_ci() |> 
  as_gt() |>
  tab_header(
    title = md("**Prevalence of depression among U.S. adolescents by sex**"),
    subtitle = "Data from the National Survey on Drug Use and Health, 2009"
    )

Prevalence of depression among U.S. adolescents by sex
Data from the National Survey on Drug Use and Health, 2009
Characteristic	female N = 8,443¹	95% CI²	male N = 8,719¹	95% CI²
Past-year prevalence of a Major Depressive Episode
negative	7,401 (88%)	87%, 88%	8,276 (95%)	94%, 95%
positive	1,042 (12%)	12%, 13%	443 (5.1%)	4.6%, 5.6%
¹ n (%)
² CI = Confidence Interval

Find the second level header

## Compute the 95% CI using gtsummary

Inside the code chunk, create your own version of the table — modifying the title, subtitle, and such to suit your desires.

Note

Advanced commentary for the interested

Our hand calculations (and manual coding using R) of the CI for a proportion is called the Wald Method. The gtsummary uses a different method called the Exact Method. Let’s explore the difference by considering females.

Wald Method

What is it?

The Wald method calculates the confidence interval for a proportion using the normal approximation.

How does it work?

Calculate the Proportion:
- Proportion (\(\hat{p}\)) = Number of students with past-year MDE / Total number of students.
- \(\hat{p} = \frac{1042}{8443} \approx 0.1234\) (12.34%).
Compute the Standard Error (SE):
- Standard Error \(SE = \sqrt{\frac{\hat{p}(1-\hat{p})}{n}}\).
- \(SE = \sqrt{\frac{0.1234(1-0.1234)}{8443}} \approx 0.0035\).
Determine the Z-Score:
- For a 95% confidence interval, the z-score is ~1.959964.
Calculate the Confidence Interval:
- Lower bound: \(\hat{p} - 1.959964 \times SE\).
- Upper bound: \(\hat{p} + 1.959964 \times SE\).
- Lower bound: \(0.1234 - 1.959964 \times 0.0035 \approx 0.1165\) (11.64%).
- Upper bound: \(0.1234 + 1.959964 \times 0.0035 \approx 0.1303\) (13.04%).
So, the 95% confidence interval using the Wald method is approximately [11.64%, 13.04%].

Exact Method (Clopper-Pearson Interval)

What is it?

The Exact method calculates the confidence interval directly from the binomial distribution, providing a more accurate and conservative interval, especially for small sample sizes or extreme proportions (i.e., proportions close to 0 or 1).

How does it work?

Determine the Proportion:
- As with the Wald method, the sample proportion (\(\hat{p}\)) is calculated.
- \(\hat{p} = \frac{1042}{8443} \approx 0.1234\) (12.34%).
Use the Binomial Distribution:
- The Exact method uses the properties of the binomial distribution to find the confidence interval. This involves calculating the cumulative probabilities to determine the interval bounds.
Calculate the Confidence Interval:
- In R, you can use the binom.test() function to compute this interval.
- This provides the lower and upper bounds of the 95% confidence interval, which in this case is [11.65%, 13.06%]

# Number of students with past-year MDE
positive <- 1042

# Total number of students
total <- 8443

# Perform the binomial test
result <- binom.test(positive, total, conf.level = 0.95)

# Print the result
print(result)


    Exact binomial test

data:  positive and total
number of successes = 1042, number of trials = 8443, p-value < 2.2e-16
alternative hypothesis: true probability of success is not equal to 0.5
95 percent confidence interval:
 0.1164716 0.1306211
sample estimates:
probability of success 
             0.1234158

Summary of Differences

Wald Method:
- Suitable for large sample sizes and when the proportion is not near 0 or 1.
- Simpler and faster, but less accurate for small samples or extreme proportions.
Exact Method (Clopper-Pearson):
- More accurate, especially for small samples or proportions close to 0 or 1.
- More conservative and computationally intensive, but provides a precise interval.

The Wald method is easier to compute but can be less reliable for small sample sizes or when the proportion is close to 0 or 1. The Exact method is more accurate and conservative, making it a better choice in those situations.

Step 6

Recall that in Module 7 we replicated a graph from a Journal of Adolescent Health paper by Dr. Michael Daly. We computed the proportion of adolescents who were positive for past year MDE each year from 2009 to 2019. Now, let’s update that graph to include 95% CIs for those proportions.

group.colors <- c("male" = "#6ce1ff", "female" = "#e0ce75")

for_trend_graph_summary |> 
  ggplot(mapping = aes(x = year, y = proportion_mde_pastyear_positive, group = sex, color = sex)) +
  geom_line(linewidth = 2) +
  geom_point(size = 3) +
  scale_x_continuous(breaks = 2009:2019) +
  scale_y_continuous(limits = c(0,.25), labels = scales::percent_format(accuracy = 1)) +
  theme_minimal() +
  scale_color_manual(values = group.colors) +
  labs(title = "Proportion of adolescents who met criteria for a past-year Major Depressive Episode (MDE)",
       subtitle = "Data from the National Survey on Drug Use and Health (NSDUH), 2009 - 2019",
       x = "Year", 
       y = "Percent of adolescents meeting criteria for past-year MDE",
       color = "Sex")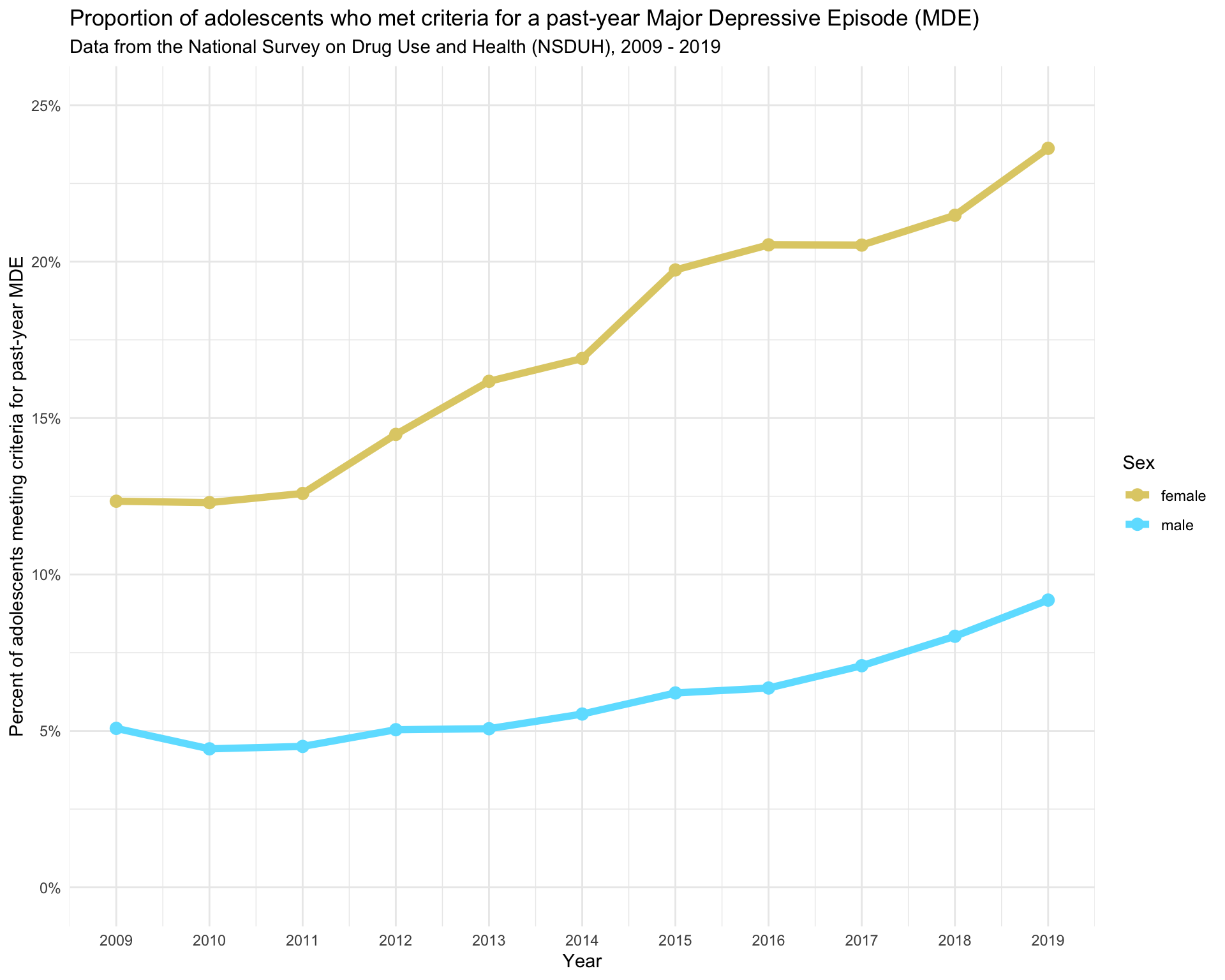

Find the first level header

# Add 95% CI to the Daly graph

And, the second level header

## Compute the CIs

Inside the code chunk, first create a data frame that includes the necessary variables. Do the following in a pipe:

Create a data frame called for_trend_graph that is based on the nsduh_20092019 data frame.
Select the following variables: year, sex, mde_pastyear.
Drop cases with missing data.

Write this part of the code — click run on the completed code chunk to make sure it executes correctly.

Now, we can summarize the variables that we need for the graph. Working in the same code chunk, create a new pipe that does the following:

In a new pipe, create a data frame called for_trend_graph_summary that is based on the for_trend_graph data frame.
Create a new variable called mde_pastyear_positive that equals 1 if the adolescent was “positive” for past-year MDE, and equals 0 if the adolescent was “negative” for past-year MDE.
Group the data frame by year and sex.
Use summarize() to create three summarized variables: proportion_mde_pastyear_positive to compute the proportion of male and female adolescents with a past year MDE for each year of the study; ci_lower to compute the lower bound of the 95% CI using the theory-based/parametric method; and ci_upper to compute the upper bound of the 95% CI using the theory-based/parametric method.

Step 7

Find the second level header

## Recreate the graph with the 95% CIs

Inside the code chunk, update the graph that we created to replicate the Daly paper – but add the 95% CIs. These are added by including the following as an additional geometry:

geom_errorbar(mapping = aes(ymin = ci_lower, ymax = ci_upper), width = 0.2) +

When finished, write a few sentences to describe the graph and provide your insight.

Step 8

Find the second level header

## Recreate the graph with the 95% CIs -- account for the sampling design and the survey weights

Inside the code chunk, copy and paste the code below. This code uses the survey package that we considered in Module 7 to create the proportion of adolescents with a past year MDE and the corresponding 95% CI by sex and age, adjusting for the sampling design and the survey weights.

# Create a survey design object
df_for_weighted_20092019 <- 
  nsduh_20092019 |> 
  select(year, starts_with("mde_"), sex, adol_weight, vestr, verep) |> 
  mutate(mde_pastyear_positive = case_when(mde_pastyear == "positive"  ~ 1,
                                         mde_pastyear == "negative" ~ 0)) 

weighted_20092019 <-
  svydesign(
    id = ~ verep, 
        strata = ~ vestr, 
        data = df_for_weighted_20092019, 
        weights = ~ adol_weight, 
        nest = TRUE 
    )

# Calculate the weighted summary by sex and year
weighted_summary_20092019 <- 
  svyby(
    formula = ~mde_pastyear_positive,   
    by = ~year + sex,            
    design = weighted_20092019,       
    FUN = svymean,           
    na.rm = TRUE              
  ) |> 
  as.data.frame()

weighted_summary_20092019

Notice that the data frame called weighted_summary_20092019 has a column called se. In addition to creating a estimate of the proportion of adolescents with a past-year MDE by sex and year, the svydesign() function also computes a standard error for each proportion which accounts for the sampling design and survey weights.

Add to the pipe that creates weighted_summary_20092019. After the as.data.frame() call, add a pipe operator, return to a new line, then use the columns mde_pastyear_positive and se to compute two new columns that capture the lower and upper bounds of the 95% CI.

Finally, use this updated version of weighted_summary_20092019 to recreate the line graph with error bars based on these weighted estimates. Use a title/subtitle or caption to indicate that the estimates and CIs have been adjusted to account for the sampling design of the NSDUH.

Step 9

Finalize and submit.

Now that you’ve completed all tasks, to help ensure reproducibility, click the down arrow beside the Run button toward the top of your screen then click Restart R and Clear Output. Scroll through your notebook and see that all of the output is now gone. Now, click the down arrow beside the Run button again, then click Restart R and Run All Chunks. Scroll through the file and make sure that everything ran as you would expect. You will find a red bar on the side of a code chunk if an error has occurred. Taking this step ensures that all code chunks are running from top to bottom, in the intended sequence, and producing output that will be reproduced the next time you work on this project.

Now that all code chunks are working as you’d like, click Render. This will create an .html output of your report. Scroll through to make sure everything is correct. The .html output file will be saved along side the corresponding .qmd notebook file.

Follow the directions on Canvas for the Apply and Practice Assignment entitled “NSDUH Confidence Intervals Apply and Practice Activity” to get credit for completing this assignment.