| Variable | Description |
|---|---|
| cz_name | The name of the commuting zone. |
| state | The state the commuting zone belongs to. |
| abs_up_mobility | The mean income rank of children with parents in the bottom half of the income distribution. |
| seg_racial | The Thiel index of racial segregation (a higher score means more segregation). |
| gini | The Gini Coefficient, a measure of income inequality. The measure ranges from 0 (representing perfect equality) to 100 (representing perfect inequality). |
| test_scores_incadj | Income adjusted standardized test scores for students in grades 3 through 8. |
| social_capital_index | A computed index comprised of voter turnout rates, the fraction of people who return their census forms, and various measures of participation in community organizations. |
| frac_singlemother | The proportion of households headed by a single mother. |
Apply and Practice Activity
Introduction to Model Building
Introduction
In predictive analytics, an analyst aims to construct a model that not only fits the existing data well but also exhibits strong predictive accuracy on new, unseen data. Achieving this requires striking a delicate balance; a model should be sensitive enough to capture underlying patterns in the training data without becoming so specific that it performs poorly on fresh data — a phenomenon known as overfitting. To navigate this challenge, one of the cornerstone techniques involves dividing the data frame into two distinct parts: a training set and a test set.
Why Split the Data?
Guided Model Development: Using the training set, we shape and refine our model, adjusting its parameters and structure to best capture the known outcomes in this subset of the data.
Objective Evaluation: The test set, kept separate from all training processes, acts as new, unseen data for the model. By evaluating the model’s performance on this set, we obtain a more objective measure of its predictive accuracy, providing insights into how it might perform in real-world scenarios.
Mitigating Overfitting: By training on one subset and testing on another, we can detect and mitigate overfitting. A model that performs exceptionally well on the training data but poorly on the test data is likely too tailored to the specificities of the training data and might not generalize well.
Enhancing Robustness: This two-step process — training on one set and validating on another—ensures the model’s robustness. It reduces the chances of the model being overly influenced by quirks or anomalies in the data, leading to a model that’s more reliable and versatile.
In conclusion, the practice of splitting data into a training and test set is more than just a procedural step; it’s a strategic move to build models that are both accurate and robust, ready to tackle real-world predictive challenges with confidence.
The focus for the activity
In this Apply and Practice Activity, we will study the model building and validation process using a straight-forward approach and a relatively simple example. We will use data from a study conducted by Raj Chetty, Ph.D. and colleagues. The academic paper describing the study we’ll consider can be downloaded here.
Briefly, Chetty and colleagues compiled administrative records on the incomes of more than 40 million children and their parents to quantify social mobility across areas within the U.S. — called commuting zones. One of the key findings of the study is the substantial variability in social mobility across the U.S. For example, the authors found that the likelihood that a child reaches the top quintile (i.e., the top 20%) of the national income distribution starting from a family in the bottom quintile (i.e., the bottom 20%) is 4.4% in Charlotte, NC but 12.9% in San Jose, CA.
In the final aim of the Chetty and colleague’s paper, the authors examined factors correlated with upward mobility. They found that high upward mobility areas have (1) less residential segregation, (2) less income inequality, (3) better primary schools, (4) greater social capital, and (5) greater family stability.
The data frame that you will explore today includes data on 709 commuting zones. There is an outcome variable (abs_up_mobility of the commuting zone) and a set of predictors that characterize the commuting zone.
In this activity we will build a model to predict absolute upward mobility (abs_up_mobility) with the five key predictors outlined by Chetty and colleagues: seg_racial, gini, test_scores_incadj, social_capital_index, frac_singlemother.
Please follow the steps below to complete this activity.
Step by step directions
Step 1
In the Posit Cloud foundations project, navigate to the apply_and_practice folder in the programs folder of the course project. Open up the file called intro_model_building.qmd.
To ensure you are working in a fresh session, close any other open tabs (save them if needed). Click the down arrow beside the Run button toward the top of your screen then click Restart R and Clear Output.
Step 2
First we need to load the packages that are needed for this activity. Find the first level header called
# Load packages
Inside the code chunk load the following packages: vip, skimr, tidymodels, broom, here, tidyverse.
Step 3
Find the first level header
# Import data
Inside the code chunk, import the data frame (chetty_cov.Rds), name it chetty_cov.
Click run on this code chunk and inspect the data frame. Reconcile it with the description of variables above to familiarize yourself with the variables and data frame.
Step 4
Under the first level header
# Prepare the data
Inside the code chunk, select the following variables: abs_up_mobility, seg_racial, gini, test_scores_incadj, social_capital_index, frac_singlemother. Then use drop_na() to remove cases with missing data on any of the included variables. Call the new data frame df. Notice how many cases were dropped.
In addition, create z-scores for all 5 predictors. You can do this all at once using the across() function from dplyr.
mutate(across(.cols = c(seg_racial, gini, test_scores_incadj, social_capital_index, frac_singlemother),
~ ( . - mean(.) ) / sd(.)))Here’s a breakdown of the across() function in this context:
- The across() function, when used within mutate(), allows for applying transformations to multiple columns. The columns to be transformed are listed as the first argument to across() (i.e.,
.cols = ()). - The transformation applied to each of these columns is specified by the formula:
~ (.-mean(.))/sd(.). Here, the.is a placeholder that represents the current column being processed. So, this tells R to take each variable, subtract the mean of the variable, then divide by the standard deviation of the variable. - By applying this transformation, these five variables are converted to z-scores. You can verify this transformation by inspecting the data frame, or using tools like skim() to confirm that each of these columns now has a mean of 0 and a standard deviation of 1.
- Note that in this code, the original variables will be overwritten with the z-score version, which is okay in this instance since we won’t use the untransformed variables.
Step 5
Next, we will split the data frame into a training data frame and a testing data frame.
Under the first level header
# Split the data
Inside the code chunk, use the tidymodels package to split the data frame into a training data frame and a test data frame. Copy and paste the code below into your analysis notebook.
set.seed(8675309)
data_split <- initial_split(df, prop = 0.8)
train_data <- training(data_split)
test_data <- testing(data_split)Here’s a breakdown of what is happening this code chunk.
The set.seed() function is used to set the random seed in R. This is important when you are splitting your data into a training set and a test set, because it ensures that the same observations are always assigned to the training set and the test set. This is important for reproducibility, because it means that you can get the same results every time you run your code.
initial_split() function:
This function is used to create a single binary split of the data frame.
In the code provided, df is our data frame that we seek to split.
The
prop = 0.8argument indicates that 80% of the data will be allocated to the training set, and the remaining 20% will be allocated to the testing set.
training() and testing() functions:
After creating the initial split, the training() function is used to extract the training portion of the split data, which is 80% in this case.
Similarly, the testing() function is used to extract the testing portion, which is the remaining 20%.
Result:
After executing the code, you’ll have two separate data frames: train_data and test_data.
train_data will contain 80% of the original data, intended for training a model.
test_data will contain the remaining 20%, intended for evaluating the model’s performance on unseen data.
Once your code is written, click run and then inspect the two new data frames.
Step 6
Under the first level header
# Fit the model to training data
and the second level header
## Fit a full model
Inside the code chunk, fit a full model with the training data (that is, a model with all 5 predictors) — regress abs_up_mobility on seg_racial, gini, test_scores_incadj, social_capital_index, frac_singlemother. Name the fitted model lm_train_full. Use tidy() and glance() to examine the results of the fitted model.
Write a few sentences to describe the model output.
Step 7
Notice that in the model fit for lm_train_full, the regression coefficient for test_scores_incadj is very small. We might wonder if this variable is needed.
A parsimonious regression model is one that is as simple as possible while still capturing the underlying patterns in the data. There are a couple of primary reasons why we aim for such models:
Understandability: Simpler models are generally easier to interpret and explain. When a model is straightforward, it’s more accessible to stakeholders and easier to communicate its findings.
Bias-Variance Tradeoff: In statistical modeling, there’s a tradeoff between bias (how far off our model’s predictions are from reality) and variance (how much our model’s predictions would change with a different training set). Overly complex models may fit our current data very closely, reducing bias, but at the cost of being overly sensitive to noise. This means they might perform poorly on new, unseen data, a problem known as overfitting. On the other hand, overly simple models might not capture all the important patterns, missing out on crucial information and producing a biased assessment of what’s happening in the population. A parsimonious model strikes a balance between these two extremes, ensuring consistent and reliable predictions across different random samples of data.
In essence, we seek parsimonious models to ensure that our predictions are both understandable and generalizable, while minimizing potential errors from bias and variance.
Step 8
Calculate variable importance.
As one step to evaluate whether all predictors are needed, let’s compute a variable importance graph based on the model. We can use the vip package for this.
Variable Importance Plot (VIP):
A Variable Importance Plot (VIP) is a graphical representation that displays the importance of predictors in a model. The higher the VIP score for a predictor, the more important that predictor is in contributing to the model.
Here are the primary components and insights you can gather from a VIP:
y-axis (Variable Names): This axis lists all the predictors in the model.
x-axis (Importance Score): This axis quantifies the importance of each predictor. A larger score indicates higher importance. Typically, predictors that have a score greater than 1 are considered important.
bars: Each predictor has a corresponding bar, the length of which represents its importance. The longer the bar, the more important the predictor.
Interpretation:
Higher Scored Predictors: Predictors with scores significantly larger than 1 are those that the model heavily relies upon. Removing or altering these predictors might significantly impact the model’s performance.
Lower Scored Predictors: Predictors with scores close to or less than 1 may not add much value to the model. In some cases, removing these predictors might simplify the model without sacrificing much predictive power.
Why use VIP?
Comparison across Models: The VIP can be used to compare the importance of predictors across different types of models, not just within one model. This is especially useful when you’re trying to determine which predictors are consistently influential across different modeling techniques.
Model Simplification: By identifying predictors with low importance, you might be able to simplify your model by removing them without losing much accuracy.
Let’s calculate the VIP for our example.
Under the second level header
## Compute a variable importance graph
In the code chunk use the vip() function to create the graph. Your code should look like this:
lm_train_full |> vip()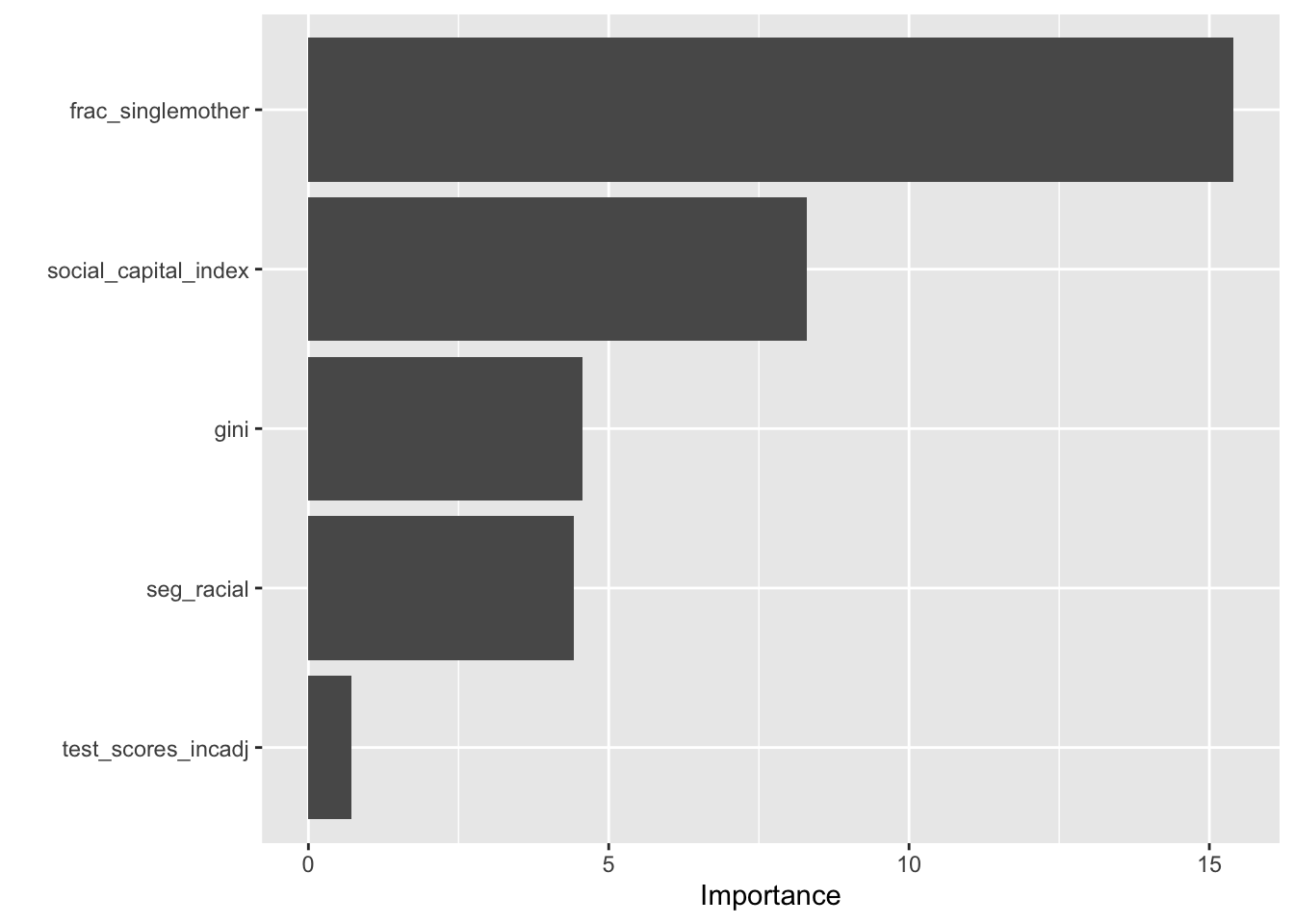
The graph suggests that test_scores_incadj has limited importance in the model.
Step 9
In an effort to obtain the most efficient model possible, let’s examine a second model that trims test_scores_incadj.
Under the second level header
## Fit a trimmed model
In the code chunk, fit a second model that trims test_scores_incadj. Name this model lm_train_trim. Use tidy() and glance() to examine the results.
Step 10
Compare the full and trimmed models.
Let’s determine if removing this variable has eroded the model fit.
First, we can compare fit indices across the two models. From the glance() output, good candidates include \(R^2\), adjusted \(R^2\), and Sigma.
\(R^2\) (R-squared):
Description: Often termed as the coefficient of determination, it measures the proportion of the variance in the dependent variable that is predictable from the independent variables.
Interpretation: An \(R^2\) of 1 indicates that the regression predictions perfectly fit the data. An \(R^2\) of 0 indicates that the model does not fit the data at all. In general, a higher \(R^2\) suggests a better fit of the model, but caution is needed: a more complex model (with more predictors) can artificially inflate the \(R^2\) value.
Adjusted \(R^2\):
Description: This is a modification of \(R^2\) that adjusts for the number of predictors in the model.
Interpretation: Unlike \(R^2\), the adjusted \(R^2\) will decrease if an irrelevant predictor is added to the model. This makes it useful for comparing models with different numbers of predictors.
Sigma:
Description: Sigma estimates the standard deviation of the residuals (errors). It gives a sense of how much, on average, the predictions deviate from the actual values.
Interpretation: A lower sigma indicates that the model’s predictions are, on average, closer to the actual values. When comparing models, if one model has a substantially lower sigma than another, it might be indicating a better fit to the data.
When comparing models, it’s crucial to consider these metrics in tandem. No single metric can provide a comprehensive view of a model’s quality, but together they can offer a clearer picture of how well the model fits the data and how it might perform on new data.
Under the second level header
## Compare full and trimmed model
In the code chunk, copy and paste the following code to compare the models. Examine the fit indices and write a few sentences about whether you feel the full or trimmed model should be retained.
# full model
lm_train_full |> glance() |> select(r.squared, adj.r.squared, sigma)
# trimmed model
lm_train_trim |> glance() |> select(r.squared, adj.r.squared, sigma)Step 11
It seems that the trimmed model is the better choice. It fits almost identically, and has fewer parameters (i.e., it’s more parsimonious). Let’s proceed with the trimmed model.
Now, that we have our model developed, we can use it to predict the outcome (abs_up_mobility) for the commuting zones in the test data frame. Importantly, the model has never “seen” the test data before. This ensures that we are evaluating its performance on new, unseen data, which provides an indication of its generalization capability.
The first step is to use the model that we developed with the training data frame (lm_train_trim) to predict the outcome (abs_up_mobility) in the test data frame.
Under the first level header
# Evaluate model performance
and the second level header
## Obtain predictions on test data frame
In the code chunk, use the following code to obtain predictions for the commuting zones in the test data frame. Here, we take the developed model from the training data frame (lm_train_trim) and apply it to the new data via the augment() function from broom. This is akin to what we did in Module 11 where we used our fitted Bread and Peace model to predict the vote share for Donald Trump in the 2020 presidential election.
The results will be stored in a data frame that we have named test_pred.
test_pred <-
lm_train_trim |>
augment(newdata = test_data)Run this code and then inspect the contents of test_pred — notice that this includes the .fitted and .resid values which represent the predicted abs_up_mobility (based on the model we developed on the training data frame) and residual (difference between the predicted and observed scores) for each commuting zone in the test data frame. Essentially, this helps us to see if our model developed with commuting zones in the training data frame can do a good job of predicting the outcome (abs_up_mobility) for commuting zones in the test data frame.
Step 12
We can generate fit metrics to determine how well our model performed in predicting the outcome in the test data frame. We’ll consider three metrics – namely \(R^2\), adjusted-\(R^2\), and Sigma. By comparing these statistics between our training and test data frames, we can gain a comprehensive understanding of how well our model generalizes to new, unseen data.
When comparing these statistics between training and test data frames, here’s what you should look for:
- \(R^2\): Ideally, the \(R^2\) values between the training and test data frames should be close. A significantly lower \(R^2\) in the test data frame might suggest that the model doesn’t generalize well to new data or may have been overfit to the training data.
- Adjusted-\(R^2\): Like \(R^2\), you’d hope the adjusted-\(R^2\) values are comparable between training and test data frames. A large drop in the test data frame might indicate overfitting.
- Sigma (Residual Standard Error): A comparable sigma between the training and test data frames is ideal. A significantly larger sigma in the test data frame suggests the model predictions are less accurate on new, unseen data.
In summary:
- Consistency between these metrics in the training and test data frames indicates good generalization and a model that’s likely not overfit.
- Significant discrepancies, especially if the test metrics are noticeably worse, suggest potential overfitting or that the model doesn’t generalize well to new data.
Let’s calcuate these metrics for our example.
Under the second level header
## Evaluate predictions
In the code chunk, use the following code to obtain commonly used evaluation metrics. Note that these calculations are the same as what we used in Module 10 to calculate the \(R^2\) manually — now we extend to also calculate the other metrics.
test_pred <-
test_pred |>
select(abs_up_mobility, .fitted, .resid) |>
mutate(for_SSR = .fitted - mean(abs_up_mobility), # calculate the difference between each predicted score and the mean of y
for_SSR2 = for_SSR^2) |> # square the difference
mutate(for_SSE2 = .resid^2) |> # square the residual
select(abs_up_mobility, .fitted, .resid, for_SSR, for_SSR2, for_SSE2)
n <- nrow(test_data) # number of cases in the test data frame
p <- length(lm_train_trim$coefficients) - 1 # number of predictors, minus the intercept in the developed model
fits_test <-
test_pred |>
summarize(SSR = sum(for_SSR2),
SSE = sum(for_SSE2),
sigma = sqrt(SSE/(n - p - 1)),
R2 = SSR/(SSR + SSE),
R2_adj = 1 - ( (n-1)/(n-p) ) * (1 - (SSR/(SSR + SSE)))
)
fits_testLet’s compare the fit metrics from the training data frame and the test data frame.
Under the second level header
## Compare fits for train and test
In the code chunk, use the code below to get a side by side comparison. Take a look at the metrics and jot down your thoughts.
# model from training data frame
lm_train_trim |> glance() |> select(r.squared, adj.r.squared, sigma)
# model from test data frame
fits_test |> select(R2, R2_adj, sigma)Step 13
Training data frame metrics
Test data frame metrics
\(R^2\): There’s a slight drop in \(R^2\) when moving from the training set to the test set, which indicates that the model might be overfitting the training data slightly, but it’s still performing reasonably well on unseen data.
Adjusted-\(R^2\): The adjusted-\(R^2\) values mirror the trend we see in \(R^2\). The values are close, suggesting that the number of predictors in the model is appropriate.
Sigma (Residual Standard Error): The residual standard error is slightly higher in the test data, which means that the model’s predictions are, on average, a bit further away from the actual outcomes in the test set than in the training set.
Thoughts: The model seems to be performing decently well. While there’s a drop in the \(R^2\) and adjusted-\(R^2\) values from the training to the test set, it’s not a drastic difference. The slight increase in sigma in the test set suggests the predictions are not as precise on the test data compared to the training data, but again, the difference isn’t extreme.
It’s worth noting that some drop in performance metrics from training to test data is typical and expected, especially if the model is complex. However, it’s always essential to be cautious about overfitting, where the model performs exceptionally well on the training data but poorly on the test data. In our example, while there’s a decrease in performance on the test data, it’s not substantial enough to be concerning.
If this simple example of model building piqued your interest — then the world of machine learning might be of interest to you. There are wonderful resources in R to conduct these types of models. The tidymodels package is the place to start.
Step 14
Finalize and submit.
Now that you’ve completed all tasks, to help ensure reproducibility, click the down arrow beside the Run button toward the top of your screen then click Restart R and Clear Output. Scroll through your notebook and see that all of the output is now gone. Now, click the down arrow beside the Run button again, then click Restart R and Run All Chunks. Scroll through the file and make sure that everything ran as you would expect. You will find a red bar on the side of a code chunk if an error has occurred. Taking this step ensures that all code chunks are running from top to bottom, in the intended sequence, and producing output that will be reproduced the next time you work on this project.
Now that all code chunks are working as you’d like, click Render. This will create an .html output of your report. Scroll through to make sure everything is correct. The .html output file will be saved along side the corresponding .qmd notebook file.
Follow the directions on Canvas for the Apply and Practice Assignment entitled “Introduction to Model Building Apply and Practice Activity” to get credit for completing this assignment.