| variable_name | label | notes |
|---|---|---|
| id | inmate ID | NA |
| years | sentence length in years | NA |
| black | race (1 = black, 0 = white) | NA |
| afro | rating for afrocentric features | inmate photo rated by ~35 CU undergraduate students; raters assigned a single, global assessment of the degree to which each face had features that are typical of African Americans, using a scale from 1 (not at all) to 9 (very much) |
| primlev | seriousness of primary offense | based on Florida’s rating system, higher numbers indicate more serious felonies |
| seclev | seriousness of secondary offense | based on Florida’s rating system, higher numbers indicate more serious felonies |
| nsecond | number of secondary offenses | NA |
| anysec | indicator for any secondary offenses (1 = yes, 0 = no) | NA |
| priorlev | seriousness of prior offenses | based on Florida’s rating system, higher numbers indicate more serious felonies |
| nprior | number of prior offenses | NA |
| anyprior | indicator for any prior offenses (1 = yes, 0 = no) | NA |
| attract | rating for attractiveness | inmate photo rated by ~35 CU undergraduate students |
| babyface | rating for babyface features | inmate photo rated by ~35 CU undergraduate students |
Apply and Practice Activity
Blair Replication — Fit the 5 Models
Introduction

Building on our replication of the Blair et al. study – this Apply and Practice Activity will walk you through fitting the five models described in the Blair and colleagues paper.
As a reminder, here is a list of the variables in the data frame:
Please follow the steps below to complete this activity.
Step by step directions
Step 1
Open up the blair_replication project in the Posit Cloud.
Step 2
In the Files tab of the lower right quadrant of RStudio, open up the blair_replication_setup.qmd document that you created earlier. Save a copy of this — call it blair_replication_fit_models.qmd (click File -> Save As…, then provide the new name). In the YAML header, change the title to: “Blair Replication: Fit the 5 Models”. We’ll do all of the work for this activity in this new version — blair_replication_fit_models.qmd.
Step 3
Click the down arrow beside Run in the top menu of the RStudio session, and then choose Restart R and Run All Chunks.
Step 4
Below the last code chunk, create a first level header called
# Prepare the final data
Then insert a code chunk.
Please do the following in the code chunk — in one pipe:
- Create a data frame called sentence, based on df.
- Center all of the following variables at their mean. Name the centered versions with the same name, but add _m — e.g.,
primlev_m = primlev - mean(primlev): primlev, nsecond, seclev, nprior, priorlev, attract, babyface, afro. - Create squared terms for the following variables: primlev_m (call it primlev2), seclev_m (call it seclev2) and priorlev_m (call it priorlev2).
- Create a variable called lnyears, which is the natural log of years.
- Create a variable called black_m as follows:
black_m = case_when(black == 0 ~ -1, black == 1 ~ 1). This will create a centered version of the indicator for race. This method is called effect coding (as opposed to dummy coding where one group is coded 1 and then reference group is coded 0). - Create a variable called race.f – it should be a factor which equals “Black” if black == 1, and “White” if black == 0.
- Select the following variables: id, years, lnyears, primlev_m, primlev2, nsecond_m, seclev_m, seclev2, nprior_m, priorlev_m, priorlev2, attract_m, babyface_m, afro_m, black, black_m, race.f.
- Use
set_variable_labels()to label all of the variables with a suitable label.
Step 5
To make sure everything is in order before we fit our models, run skim() on the sentence data frame you just created.
In your analysis notebook create a first level header called
# Obtain descriptive statistics on all key variables
Then insert a code chunk.
Inside the code chunk request skim() on the sentence data frame.
Inspect the output and make sure everything looks as you expect.
Step 6
Fit Model 1.
For Model 1, the authors regress lnyears on all of the criminal record variables, the authors describe this step by stating:
Our first analysis used multiple regression to determine the degree to which sentence length was influenced by only those factors that should lawfully predict sentencing…”
In your analysis notebook create a first level header called
# Fit the models
Then, a second level header called
## Model 1
Then insert a code chunk.
Inside the code chunk regress lnyears on primlev_m, primlev2, nsecond_m, seclev_m, seclev2, nprior_m, priorlev_m, priorlev2.
Remember that the formatted data frame is called sentence, so you’ll need data = sentence in your lm() call, not data = df.
Call the output mod1.
Call tidy() and glance() on mod1.
There is no need to interpret the slope coefficients for the control variables as these are not of substantive interest to the hypotheses of the paper – they are simply in the model to control for all of these factors that should lawfully predict sentence length before looking at our effects of interest. However, it is of interest to take a look at the \(R^2\) presented in the glance() output. It is labeled r.squared in the table above. The \(R^2\) is 0.576 – which indicates about 57% of the variability in (the natural log of) sentence length can be explained by these criminal record variables. The authors describe this model by stating:
The results of the analysis showed, as expected, that criminal record accounted for a substantial amount of the variance (57%) in sentence length.
Underneath the results of mod1, write a few sentences to describe the model that was fit, the purpose of fitting it, and the \(R^2\) in your own words.
Step 7
Fit Model 2.
In Model 2, the authors add race as an additional predictor. They describe the rational for this model by stating:
We turn next to the question of race differences in sentencing. We estimated a second model (Model 2) in which inmate race (-1 if White, +1 if Black) was entered as a predictor along with the variables from the previous model.
Thus, the null hypothesis is that there is no difference in log sentence length between Black and White inmates holding constant criminal record, and the alternative hypothesis is that there is a difference in log sentence length between Black and White inmates holding constant criminal record.
In your analysis notebook create a second level header called
## Model 2
Then insert a code chunk.
The degrees of freedom (df) for testing this effect is 206, calculated as n - 1 - the number of predictors, or 216 - 1 - 9 = 206. Inside the code chunk, Calculate the critical values of t for alpha of 0.05 (two-tailed), and thus our rejection region to test this hypothesis. If the t-statistic for the black_m slope is outside of this range (i.e., in the rejection region), then we’ll reject the null hypothesis.
Write a few sentences to describe the boundaries of the rejection region.
Now, let’s fit the model to test the hypothesis.
Inside the code chunk regress lnyears on primlev_m, primlev2, nsecond_m, seclev_m, seclev2, nprior_m, priorlev_m, priorlev2, and black_m.
Call the output mod2.
Call tidy() and glance() on mod2.
You should find that the regression coefficient for black_m is -.044. Find this in the tidy() output and note the estimate, standard error, t-statistic, and p-value for this regression slope. Because of the coding of the predictor by Blair and colleagues (-1 for White, +1 for Black), we need to perform a transformation to be able to interpret this score as the difference in lnyears for Black as compared to White inmates.
One way to interpret this is to calculate the predicted value of lnyears for White and Black inmates, holding constant all of the criminal record variables at their mean. This simplifies the calculation because all of the criminal record regression slopes are multiplied by zero (since by centering the predictors when we created the sentence data frame we’re using today we shifted the mean to 0) and thus cancel out – then we’re left simply with:
\(\widehat{y}\) = intercept + (slope_for_black_m \(\times\) black_m) that is,
\(\widehat{y}\) = 0.793318872 + (-0.043794864 \(\times\) black_m).
For White inmates:
\(\widehat{y} = 0.793318872 + (-0.043794864 \times -1) = 0.8371137\)
For Black inmates:
\(\widehat{y} = 0.793318872 + (-0.043794864\times1) = 0.749524\)
To further understand the model results, we can back transform these predicted values from ln(years) to years by exponentiating them:
# predicted years for White inmates
exp(0.8371137)[1] 2.309691# predicted years for Black inmates
exp(0.749524)[1] 2.115993Therefore, holding constant all criminal record variables at the mean in the sample, our model predicts White convicted offenders will receive 2.3 years in prison and Black convicted offenders will receive 2.1 years.
The t-statistic (labeled statistic in the output) for the regression slope for black_m is -0.884 and the p-value is 0.377. Recall that the t-statistic is calculated as the estimate divided by the standard error – and represents the number of standard errors the sample estimate is from the null hypothesis value (i.e., 0). The t-statistic is not in the rejection region, thus, we cannot reject the null hypothesis – in other words, we do not have evidence of a difference in sentence length by race.
It’s also of interest to compare the change in \(R^2\) with the addition of race. In Model 1 the \(R^2\) = 0.576, and in Model 2 the \(R^2\) = 0.577 – so, essentially the \(R^2\) is unchanged, and this corresponds with the non-significant regression slope for black_m.
The authors describe their results as follows:
The results of this analysis were consistent with the findings of Florida’s Race Neutrality in Sentencing report (Bales, 1997): The race of the offender did not account for a significant amount of variance in sentence length over and above the effects of seriousness and number of offenses.
Underneath the results of mod2, write a few sentences to describe these results in your own words.
Step 8
You might be curious about why Blair and colleagues coded the variable to compare Black and White inmates (black_m) using 1 and -1 respectively, rather than using a traditional dummy code. Had we fit the regression model using the dummy code approach (where black = 1 for Black inmates, and black = 0 for White inmates), then the regression slope would equal -0.088. This value (-0.088) represents the expected difference in sentence length in the natural log of years between Black and White inmates, holding constant criminal record.
To see that this is the case, see the results of the model below:
mod2_modified <-
lm(lnyears ~ primlev_m + primlev2 + seclev_m + seclev2 + nsecond_m + priorlev_m + priorlev2 + nprior_m +
black,
data = sentence)
mod2_modified |> tidy()mod2_modified |> glance() |> select(r.squared, sigma)The regression coefficient for black is -0.088, which indicates the expected change in the natural logarithm of sentence length when comparing Black inmates to White inmates, with all other variables held constant —- specifically, variables related to criminal records. Thus, we expect Black inmates to have a log sentence length that is 0.088 units lower than White inmates, holding the criminal record variables constant.
You might find it interesting to note that despite the difference in coding between the black dummy-coded variable in this model and the black_m effect-coded variable in the Blair and colleagues’ original model (Model 2), the t-statistics and p-values associated with these variables are identical. This is because the underlying relationship that each model is measuring — the effect of being a Black inmate versus a White inmate on sentence length — remains the same.
Effect coding (using 1 and -1) and dummy coding (using 1 and 0) are just different methods of representing categorical variables in regression models, but they don’t fundamentally change the relationships being tested. The models essentially provide the same information about the influence of race on sentencing; they just frame that information differently.
In the model with dummy coding, the regression coefficient for black reflects the difference from the reference group (White inmates) to the Black inmates. In effect coding, the coefficient for black_m reflects the deviation of Black inmates from the overall mean, which is balanced by the equal and opposite deviation of White inmates.
The key takeaway is that whether we use dummy coding or effect coding, the actual statistics that emerge from the model — like the t-statistics, p-values, and the overall model fit (e.g., \(R^2\)) — will remain the same because the statistical test is essentially testing the same hypothesis. The coding method changes only the way the variables are entered into the model, not the outcome of the hypothesis test itself. Thus, the conclusions we draw about the statistical significance of race on sentence length are consistent regardless of the coding scheme.
You might be curious as to why Blair and colleagues decided to use effect coding rather than dummy coding for race. They don’t mention this explicitly in the paper – however, it’s likely because later in the paper they interact race with Afrocentric features to determine if there is effect modification (we’ll test this together in Model 4). Effect codes have some advantages over dummy codes when it comes to interpretations of models that involve interactions. This review provides additional information in case you are interested.
Step 9
In Model 3, the authors test their primary hypothesis of interest, that is, they determine if Afrocentric features predicts sentence length, holding constant race and all of the criminal record variables. The authors describe this step as follows:
In a third model, we added the degree to which the inmates manifested Afrocentric features as a predictor of sentence length, controlling for the race of the inmates and the seriousness and number of offenses they had committed.
Here, the null hypothesis is that, holding constant criminal record and race, Afrocentric features IS NOT related to log sentence length. The alternative hypothesis is that, holding constant criminal record and race, Afrocentric features IS related to log sentence length.
In your analysis notebook create a second level header called
## Model 3
Then insert a code chunk.
To begin, please calculate the rejection region for this hypothesis test. Because we’ll add an additional predictor, the df for testing this effect is 205 (we lose one additional df as compared to Model 2; n - 1 - 10 predictors). If the t-statistic for the afro_m slope is outside of this range (i.e., in the rejection region), then we’ll reject the null hypothesis.
Now, let’s fit the model.
Inside the code chunk regress lnyears on primlev_m, primlev2, nsecond_m, seclev_m, seclev2, nprior_m, priorlev_m, priorlev2, black_m, and afro_m.
Call the output mod3.
Call tidy() and glance() on mod3.
Take a look at the coefficient for Afrocentric features (afro_m), the slope estimate is 0.092.
The authors describe the effect as follows:
This analysis showed that Afrocentric features were a significant predictor of sentence length over and above the effects of the other factors.
How might this be enhanced to follow APA style? For a regression coefficient, The guidelines recommend including the estimate (b), the test statistic (t), the degrees of freedom (df), and the exact p-value, while noting the significance level. Here’s an enhanced description of the findings incorporating these elements:
This analysis revealed that Afrocentric features significantly predicted sentence length, even after accounting for the effects of criminal history and race. Specifically, for each one-unit increase in the measure of Afrocentric features, the natural log of sentence length increased by an average of 0.092 units (b = 0.092, t(205) = 2.306, p = 0.022). Additionally, the variance explained by Model 3 was 58.8% (R² = 0.588), which is an improvement over Model 2 (ΔR² = 0.011).
This is a nice resource put together by the University of Washington on writing statistical results in APA format.
Blair and colleagues go on to revisit the effect of race, holding constant Afrocentric features. Notice that the t-statistic for this slope (labeled black_m) is -2.280, which is in the rejection region and the p-value is therefore less than alpha (i.e., p = 0.024). This constitutes evidence of a significant effect of race. The slope estimate is negative (-0.161), indicating that Black inmates are given shorter sentences than White inmates holding constant criminal record and Afrocentric features. As we did for Model 2, we can calculate the predicted sentence lengths for Black and White inmates, holding constant all other predictors (including Afrocentric features) at the mean in the sample. This time I will automate the process:
y_hat_white = 0.787180648 + (-0.1609339*-1)
y_hat_white[1] 0.9481145exp(y_hat_white)[1] 2.580839y_hat_black = 0.787180648 + (-0.1609339*1)
y_hat_black[1] 0.6262467exp(y_hat_black)[1] 1.870577Holding constant all predictors at the mean in the sample, our model predicts White inmates to have a sentence length of 2.6 years and Black inmates to have a sentence length of 1.9 years.
Underneath the results of mod3, write a paragraph to describe the effect of Afrocentric features in your own words.
Step 10
Fit Model 4.
Models 4 and 5 constitute a type of sensitivity analysis. Here, the authors test how sensitive Model 3 (the primary model of interest) is to model assumptions and potential alternative explanations. Specifically in Model 4, the authors seek to determine if Model 3’s assumption that the effect of Afrocentric features on sentence length is the same for White and Black inmates is tenable. That is, Model 3 asserts a parallel slopes model – postulating that a higher score on Afrocentric features is related to a greater sentence length for both Black and White inmates. The assumption of parallel slopes can be relaxed by including an interaction term – here, we can add an interaction between black_m and afro_m to determine if the slopes differ.
The authors explain their rationale as follows:
In a fourth model, we examined whether the impact of Afrocentric features was the same for Black and White inmates by testing the interaction between Afrocentric features and race.
In your analysis notebook create a second level header called
## Model 4
Then insert a code chunk.
By adding an interaction term to our model, we lose an additional df; therefore, we need to calculate the new rejection region.
Now, let’s fit the model.
Inside the code chunk regress lnyears on primlev_m, primlev2, nsecond_m, seclev_m, seclev2, nprior_m, priorlev_m, priorlev2, and the interaction between black_m and afro_m (i.e., black_m*afro_m).
Call the output mod4.
Call tidy() and glance() on mod4.
The t-statistic for the interaction term (labeled black:afro_m) is -0.321, and the p-value is 0.748. The t-statistic is not in the rejection region, thus there is not evidence that different slopes for the effect of Afrocentric features on sentence length are needed. That is, the parallel slopes model appears to be sufficient. For both Black and White inmates — having greater Afrocentric features was associated with being given a longer sentence length. The authors describe this as follows:
This interaction did not approach significance, thus suggesting that the plotted lines in Figure 1 really are parallel: The effects of Afrocentric features on residual sentence length within the two racial groups were statistically equivalent.
Underneath the results of mod4, write a couple sentences to describe these results in your own words.
Step 11
Fit Model 5.
In the final model, the authors consider two alternative variables that could explain away the effect of Afrocentric features – attractiveness and babyish features.
In your analysis notebook create a second level header called
## Model 5
Then insert a code chunk.
In this model, 12 predictors are included, leaving 203 df (216 - 1 - 12). Calculate the rejection region.
Now, let’s fit the model.
Inside the code chunk regress lnyears on primlev_m, primlev2, nsecond_m, seclev_m, seclev2, nprior_m, priorlev_m, priorlev2, black_m, afro_m, attract_m and babyface_m.
Call the output mod5.
Call tidy() and glance() on mod5.
The t-statistics for the two alternative variables (attractiveness and babyish features) are not in the rejection region (-0.309 for attract_m and 0.743 for babyface_m); therefore, we do not find evidence that these variables are related to sentence length when holding all other variables constant. Moreover, the effect of Afrocentric features, remains significantly related to sentence length (i.e., the t-statistic (2.328) is in the rejection region) even after we account for attractiveness and babyish features. This provides evidence that these alternative variables cannot explain away the effect of Afrocentric features.
Underneath the results of mod5, write a few sentences to describe these results in your own words.
Step 12
To summarize, let’s create tables and figures to describe the results.
First, we can produce a figure that presents the results from the primary model (Model 3). Let’s explore a few different options. First, let’s look at a dot and whisker plot of regression estimates using the plot_model() function from the sjPlot package. This is a great way to show results in a way that depicts both the point estimate and the confidence interval for each effect. If the confidence interval does not intersect the vertical line at 0 on the x-axis (denoting a null effect), then the effect is statistically significant (i.e., the null hypothesis for the effect can be rejected, in other words, 0 is not a plausible value for the effect).
In your analysis notebook create a second level header called
## A dot and whisker plot of Model 3
Then insert a code chunk.
Inside the code chunk, insert the following code.
sjPlot::plot_model(mod3, ci.lvl = 0.95, show.values = TRUE, show.p = FALSE,
axis.title = "Regression estimates and 95% confidence intervals",
title = "Regression estimates for prediction of log sentence length in Model 3") 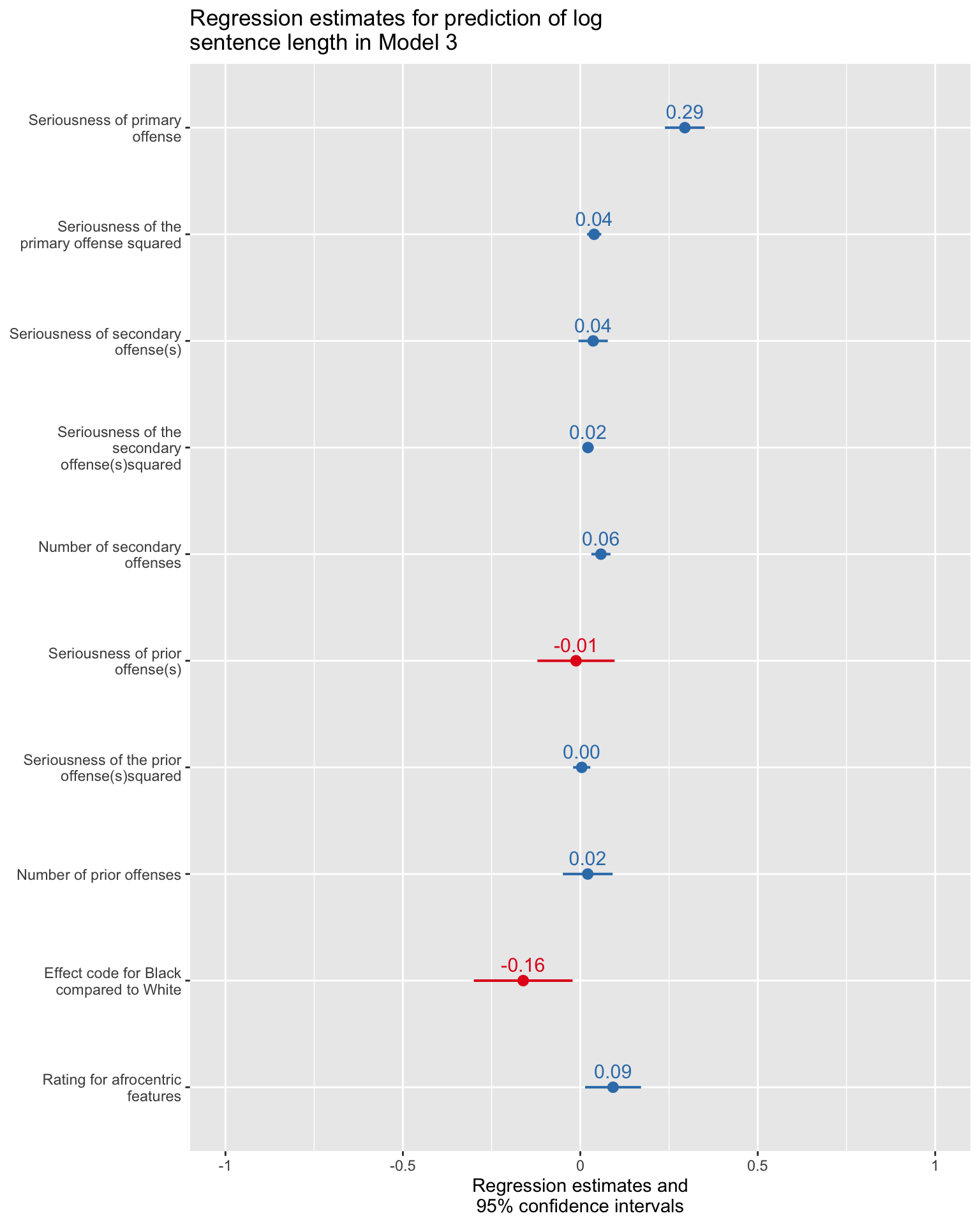
Notes for the graph: 95% confidence intervals that do not cross 0 are statistically significant. Colors denote direction of effect, with red lines denoting predictors associated with a smaller sentence length and blue lines denoting predictors with a larger sentence length.
Step 13
If you prefer a more traditional table, the tbl_regression() function from gtsummary can also create a table for you. In the Blair and colleagues paper, they present a table that provides the results of Model 1 and Model 3. Let’s replicate that. You first create two tables using tbl_regression(), then you can merge them together using tbl_merge().
In your analysis notebook create a second level header called
## A table of Models 1 and 3
Then insert a code chunk.
Inside the code chunk, insert the following code.
t1 <- mod1 |> tbl_regression(intercept = TRUE) |>
modify_header(label = "**Term**", estimate = "**Estimate**")
t3 <- mod3 |> tbl_regression(intercept = TRUE) |>
modify_header(label = "**Term**", estimate = "**Estimate**")
merged_table <-
tbl_merge(tbls = list(t1, t3),
tab_spanner = c("**Model 1**", "**Model 3**"))
final_table <-
merged_table |>
as_gt() |>
tab_header(
title = md("**Table 2. Regression estimates and 95% confidence intervals for Models 1 and 3**")
)
final_table| Table 2. Regression estimates and 95% confidence intervals for Models 1 and 3 | ||||||
|---|---|---|---|---|---|---|
| Term |
Model 1
|
Model 3
|
||||
| Estimate | 95% CI | p-value | Estimate | 95% CI | p-value | |
| (Intercept) | 0.80 | 0.61, 0.99 | <0.001 | 0.79 | 0.60, 0.98 | <0.001 |
| Seriousness of primary offense | 0.30 | 0.24, 0.35 | <0.001 | 0.29 | 0.24, 0.35 | <0.001 |
| Seriousness of the primary offense squared | 0.04 | 0.02, 0.06 | <0.001 | 0.04 | 0.02, 0.06 | <0.001 |
| Seriousness of secondary offense(s) | 0.04 | -0.01, 0.08 | 0.089 | 0.04 | -0.01, 0.08 | 0.086 |
| Seriousness of the secondary offense(s) squared | 0.02 | 0.01, 0.04 | 0.009 | 0.02 | 0.01, 0.04 | 0.008 |
| Number of secondary offenses | 0.06 | 0.03, 0.09 | <0.001 | 0.06 | 0.03, 0.09 | <0.001 |
| Seriousness of prior offense(s) | -0.01 | -0.12, 0.09 | 0.8 | -0.01 | -0.12, 0.10 | 0.8 |
| Seriousness of the prior offense(s) squared | 0.00 | -0.02, 0.03 | 0.7 | 0.00 | -0.02, 0.03 | 0.7 |
| Number of prior offenses | 0.02 | -0.05, 0.09 | 0.5 | 0.02 | -0.05, 0.09 | 0.6 |
| Effect code for Black compared to White | -0.16 | -0.30, -0.02 | 0.024 | |||
| Rating for afrocentric features | 0.09 | 0.01, 0.17 | 0.022 | |||
| Abbreviation: CI = Confidence Interval | ||||||
Step 14
Last, Blair and colleagues include a figure that presents the results of Models 2 (i.e., the model with race) and 3 (i.e., the model with race and Afrocentric features). We can create a similar figure using ggplot2. This is somewhat advanced, and so if you aren’t ready to digest it or aren’t interested you can ignore the code. However, if you are interested, you can take a look at the code needed to reproduce the plot.
In your analysis notebook create a second level header called
## A figure of the fitted model
Then insert a code chunk.
Inside the code chunk, insert the following code.
# create residual for lnyears
r.lnyears <-
lm(lnyears ~ primlev_m + primlev2 + seclev_m + seclev2 + nsecond_m + priorlev_m + priorlev2 + nprior_m, data = sentence) |>
augment(data = sentence) |>
select(id, .resid) |>
rename(resid.lnyears = .resid)
# create residual for afrocentric features
r.afro <-
lm(afro_m ~ primlev_m + primlev2 + seclev_m + seclev2 + nsecond_m + priorlev_m + priorlev2 + nprior_m, data = sentence) |>
augment(data = sentence) |>
select(id, .resid) |>
rename(resid.afro = .resid)
# merge residuals together
plot_df <- sentence |>
left_join(r.lnyears, by = "id") |>
left_join(r.afro, by = "id") |>
mutate(black.f = factor(black_m, levels = c(-1, 1), labels = c("White", "Black")))
# get hex codes for chosen palette
# RColorBrewer::brewer.pal(3, "Dark2")
# create plot
plot_df |>
ggplot(mapping = aes(x = resid.afro, y = resid.lnyears)) +
geom_point(mapping = aes(color = black.f)) +
geom_hline(yintercept = -0.044*-1, color = "#1B9E77", linetype = "dashed") + # line for whites in model 2
geom_hline(yintercept = -0.044*1, color = "#D95F02", linetype = "dashed") + # line for blacks in model 2
geom_abline(intercept = -0.161*-1, slope = 0.092, color = "#1B9E77") + # line for whites in model 3
geom_abline(intercept = -0.161*1, slope = 0.092, color = "#D95F02") + # line for blacks in model 3
theme_bw() +
theme(plot.caption = element_text(hjust = 0)) +
labs(title = "Figure 2: Model fitted results for Models 2 and 3",
x = "Afrocentric features residual", y = "Total prison time residual",
color = "Race",
caption = "Residualized sentence length and residualized Afrocentric features for Black (in orange) and White (in green) inmates. \nDashed lines denote difference in sentence length between Black and White inmates. \nSolid lines denote fitted regression line for effect of Afrocentric features on sentence length from Model 3.") +
scale_color_brewer(palette = "Dark2")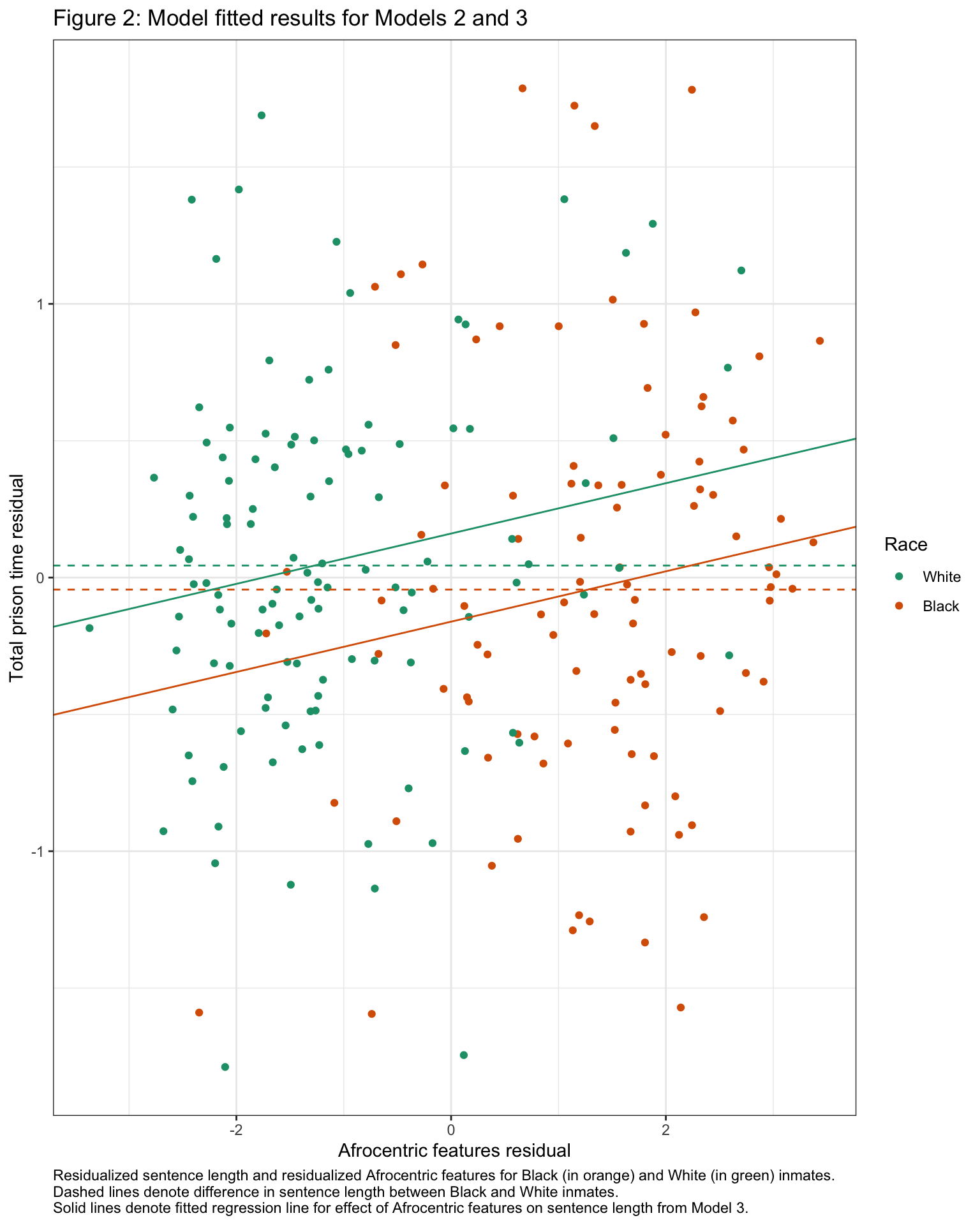
In this plot, the vertical difference in the dashed lines represents the differences in log sentence length between White and Black inmates adjusting for criminal record, but not adjusting for Afrocentric features. The difference in the solid lines represent the difference in log sentence length between White and Black inmates adjusting for criminal record and Afrocentric features. The solid lines representing the effect of Afrocentric features are parallel (i.e., a parallel slopes model), emphasizing that possessing more Afrocentric features is associated with a longer sentence length for both White and Black offenders.
Underneath the graph, write a few sentences to describe the graph as you might in an academic paper. Walk the reader through the graph with detail.
Step 15
Recall that in Modules 13 and 14, we explored the use of the marginaleffects package for visualizing the results of fitted models. For this final Step, you will create a prediction grid and generate plots based on a fitted model. Here are the general steps you need to follow:
Generate Predictions: Use the marginaleffects package to create a grid of predicted values from your fitted model. Consider how to specify the new data for which you want predictions, ensuring you cover the range of interest for your predictors. You should created predicted scores for lnyears for the range of observed afro_m, and for both Black and White inmates.
Visualize the Predictions: Create a visualization to illustrate the effects of Afrocentric features on sentence length (in years) for Black and White inmates. Hold all other covariates constant at the mean in the sample.
Customize Your Plot: Enhance the readability and presentation of your plots. Use appropriate labels, titles, and color schemes to distinguish different groups or conditions in your data.
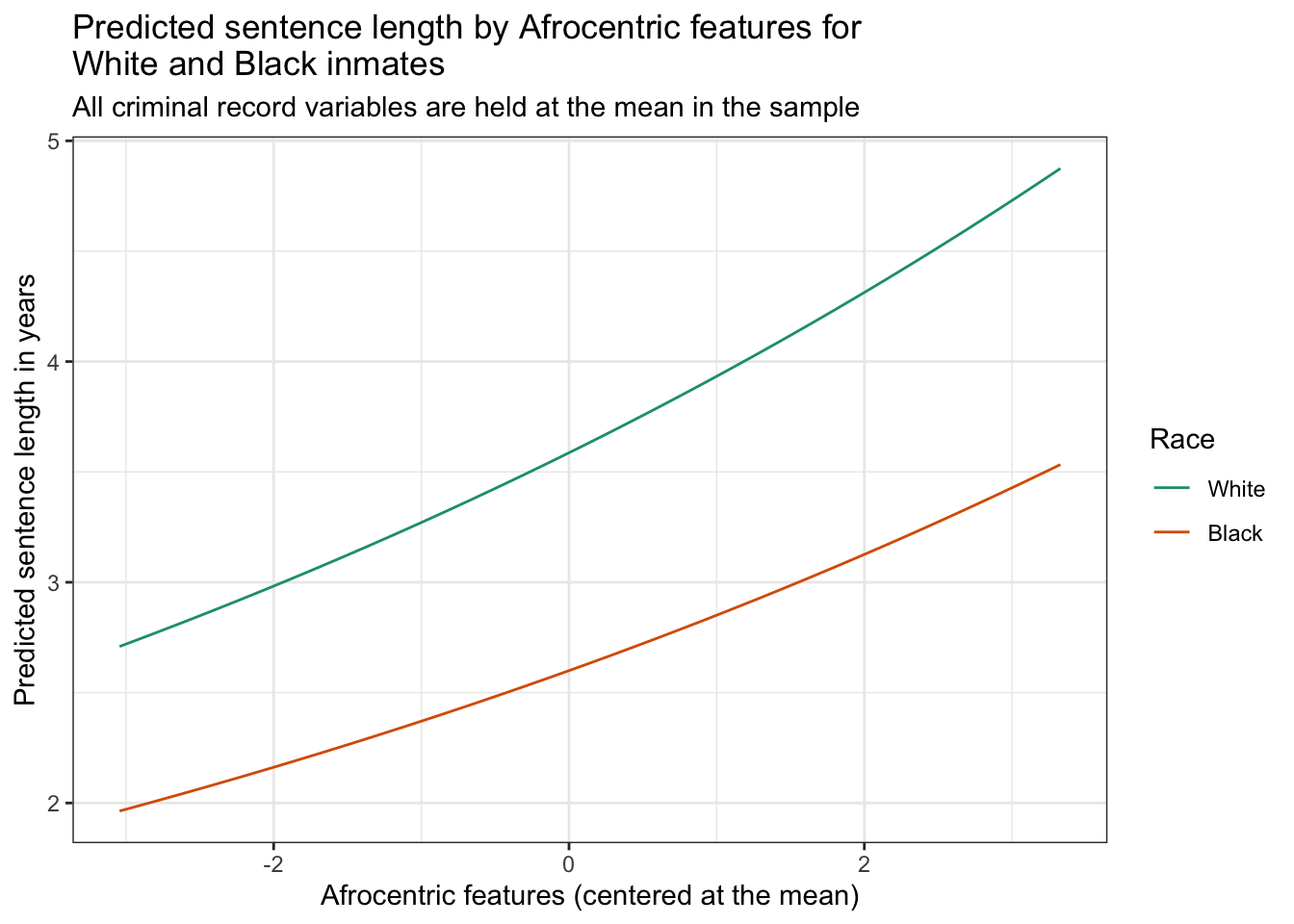
Underneath the graph, write a few sentences to describe the graph as you might in an academic paper. Walk the reader through the graph with detail.
Step 16
Now that you’ve completed all tasks, to help ensure reproducibility, click the down arrow beside the Run button toward the top of your screen then click Restart R and Clear Output. Scroll through your notebook and see that all of the output is now gone. Now, click the down arrow beside the Run button again, then click Restart R and Run All Chunks. Scroll through the file and make sure that everything ran as you would expect. You will find a red bar on the side of a code chunk if an error has occurred. Taking this step ensures that all code chunks are running from top to bottom, in the intended sequence, and producing output that will be reproduced the next time you work on this project.
Now that all code chunks are working as you’d like, click Render. This will create an .html output of your report. Scroll through to make sure everything is correct. The .html output file will be saved along side the corresponding .qmd notebook file.