A webR tutorial
Bootstrap tests for inference

The scenario
In this activity, we will work with data from this study conducted by Drs. Jake Hofman, Daniel Goldstein & Jessica Hullman. In Module 16, you studied data from their Experiment 1. Here, we’ll use data from Experiment 2.

In the experiment, participants were told they were athletes competing in a boulder sliding game against an equally skilled opponent named Blorg. The objective was to slide a boulder farther on ice than their opponent to win a 250 Ice Dollar prize, awarded to the contestant with the longest slide. They had the option to rent a “special boulder” — a potentially advantageous (but not guaranteed) upgrade expected to improve their sliding distance in their final competition. Participants then saw a visualization with statistics comparing the standard and special boulders. After studying the randomly selected visualization, the participants indicated how much they would be willing to pay for the special boulder and estimated their probability of winning with it.
Participants were randomly assigned to see one of the following visualizations that they could use to decide how much to pay for the special boulder and how certain they were that it would help them win. These four visualization types are shown below:
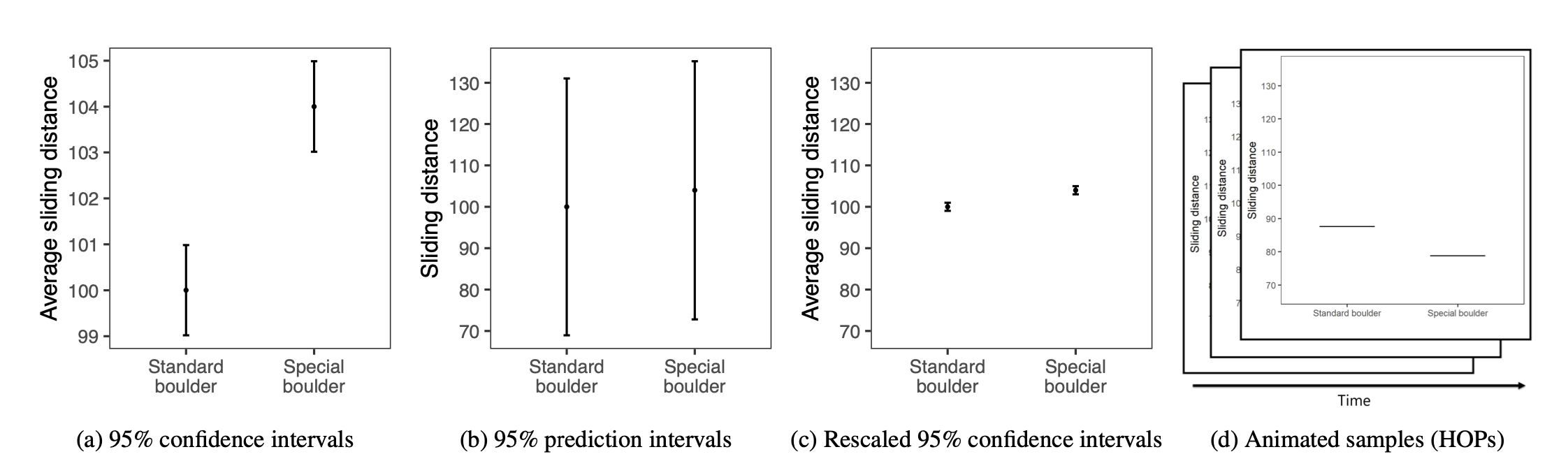
The conditions, moving from left to right, are described as:
- A 95% Confidence Interval (CI)
- A 95% Prediction Interval (PI)
- A rescaled 95% CI (CI_rescaled, i.e, the y-axis is rescaled to have the same range as the PI graph)
- Hypothetical Outcomes Plots (HOPS), which show uncertainty through a series of animated frames that depict samples from underlying distributions.
Additionally, participants were randomly assigned to see either a small effect (probability of winning with the special boulder = 0.57, where 0.5 indicates even odds) or a large effect (probability of winning with the special boulder = 0.76). In this activity, we’ll focus on the participants who were randomly assigned to see visualizations depicting a large effect size.
Import the data
Please click Run Code on the code chunk below to import the data for Experiment 2 from the Hofman et al. study.
We’ll consider two variables in this activity:
graph_type provides the type of graph the participant viewed — this is the randomly assigned condition. The types are called CI, PI, CI rescaled, and HOPS (corresponding to the descriptions above).
The outcome that we will consider here is called superiority_special. It ranges from 0 to 100 and represents the participant’s perceived probability that the special boulder would help them win the game.
Graph the results
Click Run Code on the code chunk below to create a graph of the results of the experiment.
In this graph:
Each point represents the average perceived probability that the special boulder would help a player win based on the graph type viewed.
Error bars show the 95% confidence interval around each mean, helping us understand the range within which the true mean for each group likely falls.
The blue dashed line represents the “true” probability of superiority for the special boulder (0.76). This line acts as the reference point, showing the actual effectiveness of the special boulder. By comparing each point to the blue dashed line, we can easily see if certain graph types led participants to view the special boulder as more or less effective than it actually is.
Goal of this activity
In this activity, we will explore hypothesis testing with a specific focus on assessing whether the observed average superiority rating for the special boulder for a particular graph type differs from the “true” superiority score of 0.76.
To test this, we’ll:
Select a graph type, and then calculate the mean superiority rating.
Use a bootstrapping approach to determine whether the mean superiority rating is significantly different from the “true” superiority score. We’ll use bootstrapping to empirically approximate the sampling distribution.
Through this process, we’ll interpret confidence intervals and p-values to decide whether deviations from 0.76 are statistically meaningful. This exercise will build intuition for hypothesis testing, enabling us to judge whether observed differences are likely due to random variation or reflect genuine discrepancies from the “true” superiority score.
Conduct a null hypothesis significance test using bootstrap resampling
Step 1: Choose a graph type/condition to study
- CI
- CI rescaled
- PI
- HOPS
Input the name of the graph type that you’d like to study (i.e., change graph_type == "HOPS" to your chosen graph type — for example, change “HOPS” to “CI”).
Press Run Code to create the subsetted data frame for your investigation.
Step 2: Compute descriptive statistics
What is the superiority rating for the special boulder in your selected condition?
Press Run Code on the code chunk below to compute the mean and standard deviation of the superiority score for the special boulder in your selected condition. The code also calculates the sample size.
Now, visualize the superiority score for your selected condition. Press Run Code on the code chunk below to plot the distribution of the superiority rating in the selected condition, with mean overlaid.
Step 3: Bootstrap the sampling distribution
To understand the variability of the mean superiority rating for your selected condition, we’ll create a sampling distribution using bootstrap resampling. Bootstrapping is a technique that allows us to estimate the sampling distribution by repeatedly resampling from the observed data with replacement.
Each resample generates a new sample mean, giving us a range of possible means we might expect if we repeated the study many times. This collection of resampled means forms an approximation of the sampling distribution, which helps us assess the stability and reliability of the observed mean.
Press Run Code on the code chunk below to use bootstrap resampling to compute the sampling distribution for the mean superiority rating for your selected condition.
Step 4: State the null and alternative hypothesis
The authors set the “true” superiority rating for the special boulder to a Cohen’s d of approximately 1.0, meaning that the sliding distance advantage of the special boulder over the standard boulder was about one standard deviation. As stated by the authors, this corresponds to a probability of superiority for the special boulder of 0.76.
Using this probability of 0.76 as the null hypothesis value is of interest because it represents an objectively measured “true” advantage of the special boulder. By testing whether participants’ ratings deviate from this value when exposed to different types of uncertainty visualizations, we can assess whether these visualizations might bias perceptions—either by overestimating or underestimating the actual effectiveness of the special boulder. This insight helps us understand how presentation of uncertainty affects decision-making and belief accuracy.
Thus, the hypotheses for the superiority rating for your selected condition are:
Null hypothesis: \(H_0:\small \mu = 0.76\) (the population mean for your selected condition is equal to 0.76)
Alternative hypothesis: \(H_a:\small \mu \neq 0.76\) (the population mean for your selected condition is not equal to 0.76)
Stated equivalently, we could express the null hypothesis in terms of the difference from this expected “true” value. In this case:
Null hypothesis: \(H_0: \mu - 0.76 = 0\) (the difference between the population mean and the null hypothesis mean is zero)
Alternative hypothesis: \(H_a: \mu - 0.76 \neq 0\) (the difference between the population mean and the null hypothesis mean is not zero)
This equivalent formulation emphasizes that we are testing whether the observed mean in the selected condition significantly deviates from the hypothesized value of 0.76. Both approaches ultimately test the same idea — whether the observed mean aligns with or diverges from the “true” superiority rating of the special boulder.
Visualize the null and alternative hypothesis
Press Run Code to compare the sampling distribution for the mean for your selected condition to the mean that is put forth by the null hypothesis.
Step 5: Study the sampling distribution under the null
What would the sampling distribution look like if the null hypothesis were true?
To simulate the sampling distribution under the null hypothesis (where we assume the true mean is 0.76), we can adjust each of the bootstrap resamples. Specifically, we take each resampled mean (mean_in_resample) and shift it so that it centers around the null hypothesis mean of 0.76 instead of the observed sample mean. This allows us to see what the distribution of sample means would look like if the null hypothesis were actually true.
Here’s how it works:
Calculate the Difference: We find the difference between the observed sample mean (mean_in_sample) and the desired null hypothesis mean of 0.76.
Adjust Each Resample: For each resampled mean (mean_in_resample), we subtract the observed sample mean and add 0.76. This shifts each resampled mean by the same amount so that the whole distribution centers around the null value (0.76) instead of the observed sample mean.
By creating mean_under_null, we effectively build a sampling distribution that shows what the resampled means would look like if the null hypothesis were true. This distribution can now be used to compare the extremeness of the observed mean relative to what we would expect under the null hypothesis.
Press Run Code on the code chunk below to visualize what the sampling distribution would look like if the average superiority rating for your selected condition was equal to the “true” superiority rating.
If the null hypothesis is true, how likely is it that we’d draw a random sample with the observed sample mean in your selected condition?
In order to answer this question, we can add two elements to the graph of the sampling distribution for the null hypothesis. First, we can add the 2.5th and 97.5th percentiles of the bootstrapped distribution for the null hypothesis. Second, we can add the observed sample mean (i.e., the mean superiority rating in the selected condition).
Press Run Code to add these elements.
If the null hypothesis is true, the Central Limit Theorem suggests that 95% of the random samples we would draw from the population should produce a mean that falls between the 2.5th and 97.5th percentiles of the sampling distribution (i.e., within approximately 1.96 standard errors of the null value). Drawing a sample mean outside of this range would be relatively unlikely, as it would fall into the extreme 5% of possible sample means.
Additionally, we can calculate the proportion of the null distribution that is as extreme (or more extreme) than our observed sample mean (in either direction). Press Run Code to compute these proportions.
Now, press Run Code to map these areas onto the sampling distribution under the null hypothesis.
Based on this information, does it seem likely that we would obtain a sample mean as extreme as the one observed for this condition if the null hypothesis were true?
Step 6: Query the bootstrap resamples
Using the 5000 bootstrap resamples, which have been recentered to represent the null hypothesis, we’ll identify resamples where the absolute difference between each resampled mean and the null hypothesis mean (0.76) is greater than or equal to the absolute difference between the observed sample mean and the null hypothesis mean (0.76).
What does this mean intuitively?
Imagine the null hypothesis is true: the true average rating of the special boulder’s superiority in the selected condition really is 0.76. The observed sample mean might deviate from this true value just due to random sampling error. The key question is, how unusual is the observed sample mean in your selected condition compared to what we would expect if 0.76 were the true mean?
By generating thousands of bootstrap resamples under the null hypothesis, we simulate a world where the true mean is indeed 0.76. For each resample, we calculate the mean and see how far it is from 0.76. Then, we check if this “simulated” difference is as extreme (or more extreme) than the actual difference observed in the sample for the condition you selected.
Since we’re not predicting whether the sample mean should be higher or lower than 0.76 (only that it should differ), we use absolute differences. This approach allows us to measure both unusually high and unusually low values relative to 0.76.
Here’s what we need to do to accomplish this task:
Label each resample as “extreme” if its mean difference from 0.76 is at least as large as the observed sample mean’s difference.
Count the “extreme” cases to estimate the likelihood of seeing a difference as extreme as ours by chance.
If this likelihood is very small, it suggests that the observed mean difference is unlikely to have occurred if the true mean were 0.76, providing evidence against the null hypothesis.
Press Run Code to evaluate if each resample is extreme.
Press Run Code to tally the number of extreme resamples.
The tally above shows the number of extreme resamples, and the number of not extreme resamples. Next, we calculate the proportion of resamples with an extreme mean. This proportion represents the probability of observing a mean as extreme as the sample’s mean (or more extreme) if the null hypothesis were true.
Press Run Code to calculate the proportion of resamples that are labeled “extreme.”
The probability printed above represents a conditional probability — the probability that we would draw a random sample from the population that produces a mean superiority rating as extreme as, or more extreme than, the observed mean, assuming the null hypothesis is true. This probability is also known as the p-value. A smaller p-value suggests that it would be unlikely to observe the sample mean (or a more extreme mean) if the true superiority rating were indeed 0.76. Notice that this p-value is the same value that we calculated from the ECDF of the sampling distribution under the null earlier — that is, it is the sum of the two tail areas from the density graph.
To make a decision about the null hypothesis, we often compare the p-value to a predetermined significance level, known as alpha (often set at 0.05). If the p-value is less than alpha, we reject the null hypothesis, concluding that the sample provides sufficient evidence to suggest a difference from the hypothesized value of 0.76. This comparison helps us control the probability of making a Type I error, or mistakenly rejecting a true null hypothesis.
Step 7: Compute the standard deviation of the sampling distribution under the null
The standard deviation of the sampling distribution is often referred to as the standard error. This value indicates how much variation we expect in the superiority rating due to random sampling.
Press Run Code to calculate the standard error.
Step 8: Calculate a test-statistic
When analyzing sample data, we often standardize values to understand their position relative to the mean. For example, to calculate a z-score for a raw score (such as systolic blood pressure), we subtract the mean and divide by the standard deviation. A z-score of 2 indicates that the score is 2 standard deviations above the mean.
In a similar way, we can standardize a sample mean by calculating a t-statistic. This is done by dividing the difference between the observed sample mean (e.g., the average superiority rating in your chosen condition) and the null hypothesis value (0.76) by the standard error. The t-statistic tells us how many standard errors away the sample mean is from the hypothesized value under the null. For instance, a t-statistic of 2 would mean that the sample mean is 2 standard errors above the null hypothesis value.
Calculating the t-statistic allows us to evaluate how unusual or extreme the sample mean is under the null hypothesis. By comparing this t-statistic to a t-distribution, we can assess its extremeness.
The formula for the t-statistic for this example is: \(t = \frac{\bar{x} - \mu_0}{\text{SE}}\), where \(\bar{x}\) is the sample mean (i.e., in your chosen condition), \(\mu_0\) is the null hypothesis value (e.g., 0.76), and \(\text{SE}\) is the standard error.
Press Run Code on the code chunk below to calculate the t-statistic for your selected condition.
We can visually represent the calculated test statistic overlaid onto the appropriate Student’s t-distribution (i.e., with the correct degrees of freedom (df), which are calculated as \(n - 1\) for a sample mean). This will help us see where the observed t-statistic lies relative to the distribution we’d expect if the null hypothesis were true. Press Run Code to take a look.
On this graph, the dashed green lines show the critical boundaries, marking the middle 95% of the Student’s t-distribution for the given degrees of freedom (df). The orange line represents the t-statistic calculated for the sample mean in the selected condition, showing how many standard errors the sample mean is from the null hypothesis value.
If the orange line is within the boundaries of the dashed green lines, we cannot reject the null hypothesis (we have no evidence that the sample mean is different from the hypothesized value).
If the orange line is outside the boundaries of the dashed green lines, we can reject the null hypothesis (the sample mean is significantly different from the hypothesized value). In the context of our example, this would suggest that the data visualization shown to participants in the selected condition led them to perceive a probability of superiority for the special boulder that is significantly different from the hypothesized true superiority of 0.76.
Can the null hypothesis be rejected for the selected condition?
Step 9: Test the hypothesis with a one sample t-test
The bootstap method to conducting a null hypothesis significance test (NHST) represents a non-parametric approach to hypothesis testing. Now, let’s compare this with a one-sample t-test — a parametric method for testing the same hypothesis.
A one-sample t-test relies on specific assumptions about the data, primarily the normality of the sampling distribution of the mean. If the sample size is small, the data itself should ideally follow a roughly normal distribution to satisfy this assumption. However, with larger sample sizes, the central limit theorem tells us that the sampling distribution of the mean will approximate a normal distribution even if the underlying data is not perfectly normal.
If the data meets this assumption, the one-sample t-test can be a powerful and efficient way to test the hypothesis. Here’s how it works:
Calculate the Difference from the Null: First, we calculate the difference between the sample mean and the hypothesized null value (often called \(\mu_0\)), which represents the mean under the null hypothesis.
Estimate the Standard Error: We estimate the standard error (SE) of the sample mean, which tells us how much the sample mean is expected to vary just by chance. For a one-sample t-test, this is calculated as: \(SE = \frac{s}{\sqrt{n}}\), where: \(s\) is the sample standard deviation, and \(n\) is the sample size.
Compute the t-Statistic: The t-statistic measures how many standard errors the sample mean is from the null hypothesis mean (\(\mu_0\)). The formula is \(t = \frac{\bar{x} - \mu_0}{SE}\) where: \(\bar{x}\) is the sample mean, \(\mu_0\) is the hypothesized mean under the null hypothesis, \(SE\) is the standard error of the mean.
Press Run Code on the code chunk below to calculate the one-sample t-test.
Here’s a breakdown of the code:
t_test(response = superiority_special, mu = 0.76, alternative = "two-sided"): This function tests whether the mean value of superiority_special is significantly different from0.76(the hypothesized value,mu).response = superiority_specialspecifies that superiority_special is the variable we want to test.mu = 0.76sets the null hypothesis, meaning we’re testing whether the mean of superiority_special is equal to0.76.alternative = "two-sided"specifies a two-sided test, meaning we are interested in detecting whether the mean is either higher or lower than the null value.
In evaluating the output, notice the similarity between the t-statistic we calculated using bootstrapping and the t-statistic in the t_test output (labeled statistic). Also, compare the p-value from the bootstrap approach with the p-value from the t-test output (labeled p_value). Both approaches estimate the probability of observing a mean with a difference from the null as extreme as ours (or more extreme — in either direction), offering similar insights from different perspectives.
Step 10: Compute a 95% CI for the superiority score
To wrap up, let’s use the standard error from the bootstrap resamples to calculate a 95% confidence interval (CI) for the superiority score in the selected condition. This 95% CI provides a range of plausible values for the true mean superiority score in this condition, meaning that if we repeated this resampling process many times, we would expect the true mean to fall within this interval in approximately 95% of those intervals.
Notice how this bootstrap-based 95% CI compares to the 95% CI provided by the parametric t-test.