A webR tutorial

Factorial Experiments and Multiple Comparisons

The scenario

In this activity, we will work with data from this study conducted by Drs. Jake Hofman, Daniel Goldstein & Jessica Hullman. In Module 16, you studied data from their Experiment 1. Here, we’ll use data from Experiment 2.


In the experiment, participants were told they were athletes competing in a boulder sliding game against an equally skilled opponent named Blorg. The objective was to slide a boulder farther on ice than their opponent to win a 250 Ice Dollar prize, awarded to the contestant with the longest slide. They had the option to rent a “special boulder” — a potentially advantageous (but not guaranteed) upgrade expected to improve their sliding distance in their final competition. Participants then saw a visualization with statistics comparing the standard and special boulders. After studying the randomly selected visualization, the participants indicated how much they would be willing to pay for the special boulder and estimated their probability of winning with it.

Participants were randomly assigned to see one of the following uncertainty visualizations that they could use to decide how much to pay for the special boulder and how certain they were that it would help them win. These four visualization types are shown below:

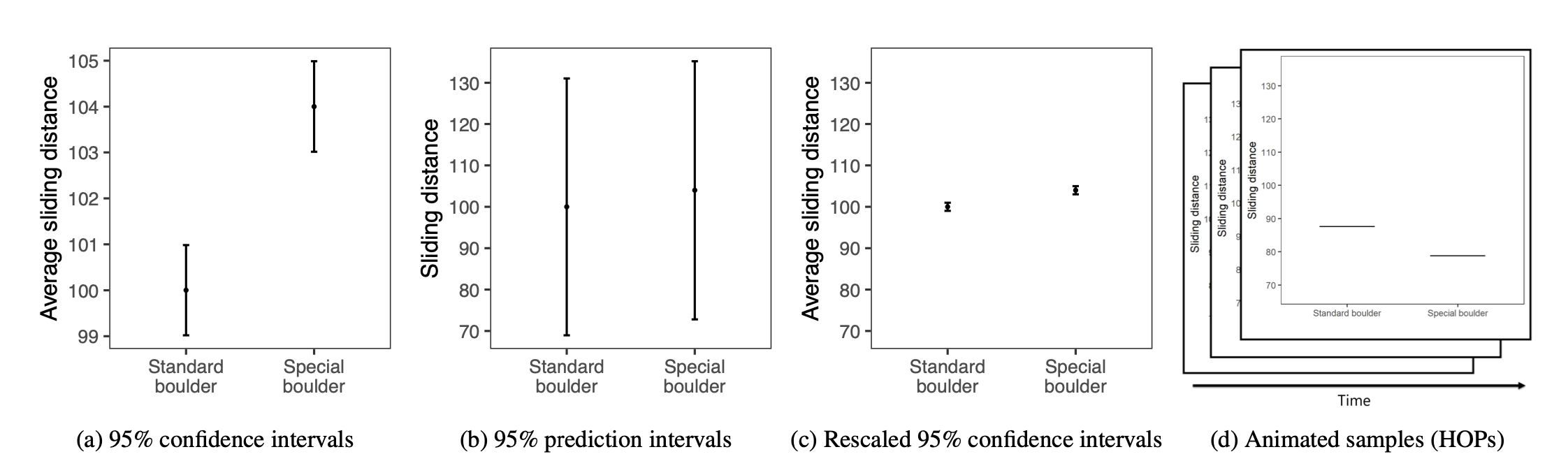
The conditions, moving from left to right, are described as:

  1. A 95% Confidence Interval (CI)
  2. A 95% Prediction Interval (PI)
  3. A rescaled 95% CI (CI_rescaled, i.e, the y-axis is rescaled to have the same range as the PI graph)
  4. Hypothetical Outcomes Plots (HOPS), which show uncertainty through a series of animated frames that depict samples from underlying distributions.

Additionally, participants were randomly assigned to see either a small effect (probability of winning with the special boulder = 0.57, where 0.5 indicates even odds) or a large effect (probability of winning with the special boulder = 0.76).

In this activity, we’ll consider the joint effect of graph type and effect size.

Import the data

Please click Run Code on the code chunk below to import the data for Experiment 2 from the Hofman et al. study.

We’ll consider three variables in this activity:

  • graph_type provides the type of graph the participant viewed — this is the randomly assigned condition. The types are called CI, PI, CI rescaled, and HOPS (corresponding to the descriptions above).

  • effect_size indicates if the graph displayed a small effect size (Cohen’s d = 0.25) or a large effect size (Cohen’s d = 1.0) for the benefit of the special boulder.

  • The outcome that we will consider here is called superiority_special. It ranges from 0 to 100 and represents the participant’s perceived probability that the special boulder would help them win the game.

Hypotheses

In this activity we will examine several general hypotheses:

  • H1: Larger effect sizes (vs. smaller ones) will generally lead to higher perceived probabilities of winning, as the expected advantage appears greater.

  • H2: Different visualization types will influence perceived probabilities, as each conveys uncertainty in a unique way. Specifically, the CI graph is expected to lead to greater misconceptions of the true superiority of the special boulder compared to the PI, CI rescaled, and HOPS graphs.

  • H3: There may be an interaction between visualization type and effect size; a certain effect size might amplify or dampen the perceived impact of graph type on the perceived superiority of the special boulder.

Modeling approach

To test these hypotheses, we will fit a linear model where the outcome variable, superiority_special, is regressed on the graph_type and effect_size factors, including their interaction.

This factorial model allows us to assess:

  • The interaction effects between graph_type and effect_size, indicating whether the effect of visualization type on perceived winning probability depends on the effect size. This helps us understand if the influence of one factor varies across the levels of the other factor.

  • Simple effects: By examining the interaction, we can explore the effect of graph_type at each level of effect_size, and vice versa. This analysis provides a more nuanced understanding of how each factor impacts participants’ perceptions within specific conditions.

Given Hypothesis 2, we’ll choose the CI graph as the reference group for graph_type. Additionally, we’ll choose the small effect size as the reference group for effect_size. To set up the factors in this way using the relevel() function, please click Run Code on the code chunk below.

Fit the model

In the code chunk below, fit a linear regression model in which superiority_special is regressed on graph_type, effect_size, and their interaction. Call the model output model. Request the tidy() and glance() output.

Since the labels of the variables plus levels are so long, the webR output is difficult to read. I will print the output in a more convenient format here:

model |> tidy(conf.int = TRUE, conf.level = .95)
model |> glance()

Interpret the model

With your neighbor, jot down the interpretation of the intercept, each slope, and the \(R^2\) from this model. Check your answers when done.

  • (Intercept): The intercept of 0.859 represents the average superiority rating for participants who viewed the CI graph under the small effect size condition (the reference group for both factors). This serves as the baseline group, meaning that participants in this group, on average, rated the probability of the special boulder helping them win at 0.859.

  • graph_typePI: Among participants who saw a small effect size, those who viewed the PI graph had a perceived probability of winning that was 0.199 lower than for those who viewed the CI graph. This indicates that, with a small effect size, the PI graph led participants to perceive less certainty in the special boulder’s advantage compared to the CI graph.

  • graph_typeCI rescaled: Among participants who saw a small effect size, those who viewed the CI rescaled graph had a perceived probability of winning that was 0.036 lower than for those who viewed the CI graph. This suggests that, with a small effect size, rescaling the CI graph slightly reduced perceived certainty compared to the standard CI.

  • graph_typeHOPS: Among participants who saw a small effect size, those who viewed the HOPS graph had a perceived probability of winning with the special boulder was 0.205 lower than those who viewed the CI graph. This effect is similar to the PI graph, indicating that, in the context of a small effect size, HOPS also led to a lower perceived advantage.

  • effect_sizeLarge effect size: Among participants who viewed the CI graph, those who saw a large effect size had a perceived probability of winning that was 0.028 higher than those who saw a small effect size. This suggests that viewing a large effect size with the CI graph slightly boosted participants’ confidence in the special boulder’s advantage.

  • graph_typePI*effect_sizeLarge effect size: The positive coefficient of 0.045 suggests that the negative impact of the PI graph (compared to the CI graph) on perceived probability that the special boulder will help one win is reduced when the effect size is large. Specifically, the difference between the PI and CI graphs decreases from -0.199 (small effect size) to -0.154 (large effect size). This indicates that the difference in perceived probability of the special boulder’s superiority between the CI and PI graphs is less when the effect size is large, meaning that the effect of graph type on participants’ perceptions is diminished at higher effect sizes. In other words, when the effect size is large, participants’ perceptions are less influenced by the type of graph they view, and the disparity between the CI and PI graphs in affecting perceived superiority is reduced. (Note that -0.199 + .045 = -0.154).

  • graph_typeCI rescaled*effect_sizeLarge effect size: The positive coefficient of 0.032 means that the slight negative impact of the CI rescaled graph is nearly eliminated when the effect size is large. The difference between the CI rescaled and CI graphs changes from -0.036 (small effect size) to -0.004 (large effect size), suggesting minimal difference between the two graphs under the large effect size condition. Note that the 95% CI for this estimate includes 0; therefore, this interaction term doesn’t quite meet the threshold of statistical significance.

  • graph_typeHOPS*effect_sizeLarge effect size: The positive coefficient of 0.064 suggests that the negative impact of the HOPS graph (compared to the CI graph) on the perceived probability that the special boulder will help one win is reduced when the effect size is large. Specifically, the difference between the HOPS and CI graphs decreases from -0.205 (small effect size) to -0.141 (large effect size). This means that participants’ perceptions of the HOPS graph become more similar to those of the CI graph under the large effect size condition, although the HOPS graph still leads to slightly lower perceived probabilities than the CI graph. The tendency for the CI graph to produce higher perceived superiority compared to the HOPS graph is attenuated when the effect size is large.

  • The \(R^2\) is 0.30, indicating that about 30% of the variability in the superiority ratings can be predicted by the two factors and their interaction.

Simple slopes

We can use the marginaleffects package to compute the simple slopes for the effect of viewing a large, versus a small, effect size across each type of graph.

Click Run Code on the code chunk below to accomplish this task.

  • Explanation: The slopes() function calculates the estimated difference in the outcome between the large and small effect sizes for each graph type.

  • Output Interpretation: The estimate column shows how much the perceived probability of winning with the special boulder changes when moving from a small to a large effect size within each graph type.

Likewise, we can compute the simple slopes for the effect of each graph type, compared to the reference graph type (CI), for both small and large effect size.

Click Run Code on the code chunk below to accomplish this task.

  • Explanation: The slopes() function calculates the difference in the outcome between each graph type and the reference graph type (CI) for both small and large effect sizes.

  • Output Interpretation: The estimate column indicates how each graph type influences the perceived probability of winning compared to the CI graph within each effect size condition. Note how these match the simple slopes that we calculated by hand in the model interpretations for the interaction effects.

Marginal slopes

We can also use the marginaleffects package to compute marginal slopes. Marginal slopes represent the average effect of one variable across the levels of other variables in the model. For example, we can compute the effect of seeing a large effect size versus a small effect size averaged over all graph types.

Press Run Code on the code chunk below to estimate the marginal slope for effect size:

This means that, on average, viewing a large effect size (compared to a small effect size) increases the perceived superiority rating by approximately 0.063, averaged over all graph types.

  • Why Compute Marginal Effects?

    Marginal effects provide a summary measure of the effect of an independent variable, averaging over the levels of other variables. This is particularly useful when interactions are present in the model, as it allows us to understand the general effect of a variable across different conditions.

  • Assessing Hypotheses:

    By computing the marginal effect of effect_size, we directly test H1. If the estimate is positive and significant, it indicates that larger effect sizes generally lead to higher perceived probabilities of winning, regardless of the graph type.

Similarly, we can compute the marginal effects for graph_type averaged over effect_size:

The results provide the average effect of each graph type compared to the reference graph type (CI), averaged over both effect sizes.

By calculating marginal slopes, we enhance our understanding of how each factor influences the outcome variable on average. It complements the interaction analysis by providing a broader view of the main effects while acknowledging the complexity introduced by the interaction.

Create a graph

To visualize our model results, we can use the marginaleffects package to create a graph of the fitted model.

To grow your understanding of the fitted model, try to map the estimates that we’ve computed in this activity onto the graph.

What about other comparisons?

While our fitted model provides valuable insights into the overall effects of graph type and effect size on the outcome, it doesn’t explicitly compare ALL individual groups. For instance, we might want to compare the mean superiority score for the PI and HOPS graph types when the effect size is large versus small. These comparisons don’t show up in our fitted model.

Pairwise comparisons allow us to directly examine these specific differences and determine if they are statistically significant. By conducting these comparisons, we can gain a more granular understanding of the relationships between our variables and identify which groups are truly different from each other.

The number of pairwise comparisons possible depends on the number of groups. We have a total of 8 groups in our study:

  1. Small effect size + CI
  2. Small effect size + PI
  3. Small effect size + CI rescaled
  4. Small effect size + HOPS
  5. Large effect size + CI
  6. Large effect size + PI
  7. Large effect size + CI rescaled
  8. Large effect size + HOPS

If we have k groups, the number of pairwise comparisons is: k * (k - 1) / 2, where k is the number of groups. Thus, there are a total of 28 possible comparisons: 8 * (8 - 1) / 2 = 28.

To make all of these pairwise comparisons, we can leverage the emmeans package. This powerful package provides a flexible framework for estimating marginal means and conducting various types of contrasts, including pairwise comparisons.

By applying the emmeans functions to our fitted model, we can obtain estimated differences in the outcome for each combination of graph type and effect size. Click Run Code on the code chunk below to accomplish this task.

The value under estimate shows the difference in the outcome (the superiority rating for the special boulder) for each listed comparison/contrast. For example, the first row indicates that the difference in the average superiority score for people who viewed a small effect size CI graph compared to a small effect size PI graph is 0.19870. The p-value for this effect is less than .0001 — indicating the probability that we’d obtain a difference of this magnitude or larger if there actually was no difference between groups. In other words, we can be confident that this difference in the superiority score is significant.

Adjusting for multiple comparisons

When we perform multiple pairwise comparisons, we increase the chance of making a Type I error. A Type I error occurs when we incorrectly reject a null hypothesis. To account for this, we need to adjust our p-values.

By default, emmeans uses the Tukey method for adjustment in this scenario. Tukey’s Honestly Significant Difference (HSD) test is a statistical procedure used to determine whether the means of different groups are significantly different from each other after fitting a model. When multiple pairwise comparisons are made between group means, the likelihood of committing a Type I error (incorrectly rejecting a true null hypothesis) increases. Tukey’s HSD addresses this issue by adjusting the significance levels to control the family-wise error rate — the probability of making one or more Type I errors across all comparisons. It does this by calculating a critical value based on the studentized range distribution, which accounts for the number of groups being compared and the variability within the data. Any difference between group means that exceeds this critical value is considered statistically significant. In the context of our example, applying Tukey’s HSD allows for all possible pairwise comparisons between the eight combinations of graph type and effect size, enabling us to identify which specific groups have significantly different perceived superiority ratings without inflating the risk of false positives due to multiple comparisons.

Why do we need to adjust p-values?

When we conduct multiple statistical tests, there’s a higher chance of finding at least one “significant” result by chance, even if no real effect exists. This is called the multiple comparisons problem. For example, if we run 20 tests, even at a 5% significance level, we’d expect around one false positive simply by chance.

Adjusting p-values, using methods like Tukey’s adjustment, helps control this problem by lowering the threshold for significance, making it harder for random chance to appear as a meaningful result. This way, we can be more confident that any significant results we see are likely due to actual effects rather than random variation.

In PSY653, you will learn about False Discovery Rate procedures in depth.