A webR tutorial

Permutation tests for inference

The scenario

In this activity, we will work with data from this study conducted by Drs. Jake Hofman, Daniel Goldstein & Jessica Hullman. In Module 16, you studied data from their Experiment 1. Here, we’ll use data from Experiment 2.

In the experiment, participants were told they were athletes competing in a boulder sliding game against an equally skilled opponent named Blorg. The objective was to slide a boulder farther on ice than their opponent to win a 250 Ice Dollar prize, awarded to the contestant with the longest slide. They had the option to rent a “special boulder” — a potentially advantageous (but not guaranteed) upgrade expected to improve their sliding distance in their final competition. Participants then saw a visualization with statistics comparing the standard and special boulders. After studying the randomly selected visualization, the participants indicated how much they would be willing to pay for the special boulder and estimated their probability of winning with it.

Participants were randomly assigned to see one of the following visualizations that they could use to decide how much to pay for the special boulder and how certain they were that it would help them win. These four visualization types are shown below:

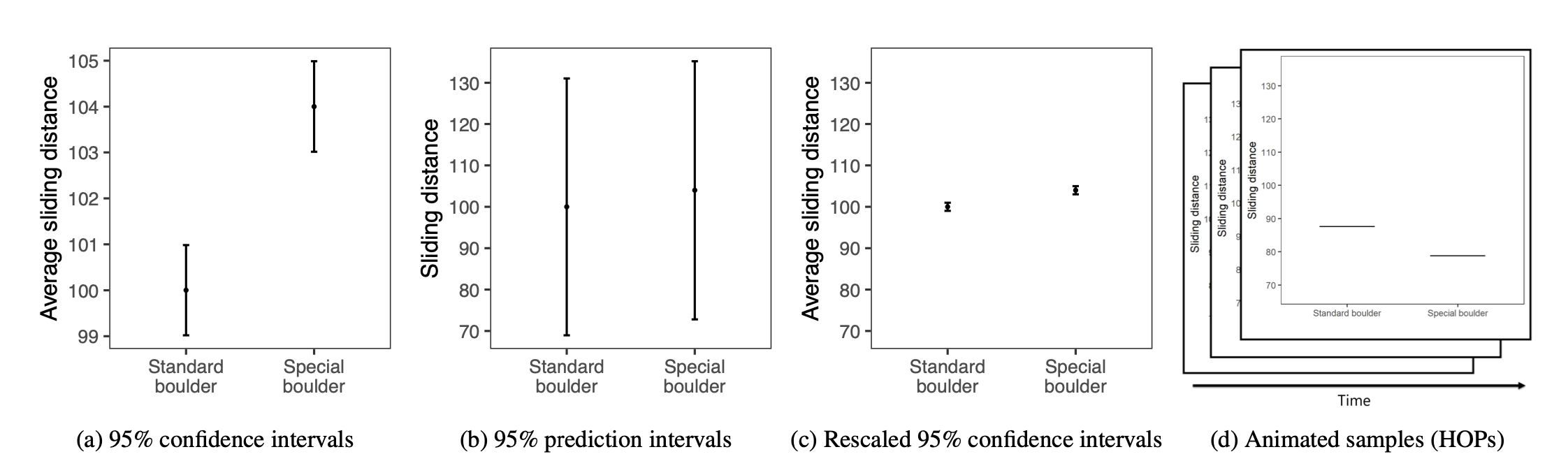
The conditions, moving from left to right, are described as:

A 95% Confidence Interval (CI)
A 95% Prediction Interval (PI)
A rescaled 95% CI (CI_rescaled, i.e, the y-axis is rescaled to have the same range as the PI graph)
Hypothetical Outcomes Plots (HOPS), which show uncertainty through a series of animated frames that depict samples from underlying distributions.

Additionally, participants were randomly assigned to see either a small effect (probability of winning with the special boulder = 0.57, where 0.5 indicates even odds) or a large effect (probability of winning with the special boulder = 0.76). In this activity, we’ll focus on the participants who were randomly assigned to see visualizations depicting a large effect size.

Import the data

Please click Run Code on the code chunk below to import the data for Experiment 2 from the Hofman et al. study.

We’ll consider two variables in this activity:

graph_type provides the type of graph the participant viewed — this is the randomly assigned condition. The types are called CI, PI, CI rescaled, and HOPS (corresponding to the descriptions above).
The outcome that we will consider here is called wtp_final. It represents the amount of money (in Ice Dollars) that the participant reported they would pay to rent the special boulder.

Graph the results

Click Run Code on the code chunk below to create a graph of the results of the experiment.

In this graph:

Each point represents the average willingness to pay for the special boulder based on the graph type viewed.
Error bars show the 95% confidence interval around each mean, helping us understand the range within which the true mean for each group likely falls.

Goal of this activity

In this activity, we will explore hypothesis testing with a specific focus on assessing whether the observed average willingness to pay for the special boulder differs significantly between conditions (i.e., type of graph viewed).

To test this, we’ll:

Select two conditions to compare (for example, those who viewed a CI graph versus a PI graph) and calculate the mean willingness to pay in each condition.
Use a permutation testing approach to determine whether the observed difference in mean willingness to pay between the two conditions is statistically significant. This method allows us to empirically approximate the distribution of differences we would expect by random chance if there were no true difference between conditions.
Through this process, we’ll interpret the resulting p-value to assess the likelihood that any observed difference is due to random variation. This exercise will build intuition for hypothesis testing and help us judge whether the observed differences in willingness to pay reflect genuine group differences or are likely due to chance.

What is a permuation test?

When we conduct a statistical test, we’re often trying to determine whether an observed result — such as a difference in willingness to pay for the special boulder between experimental conditions — could have occurred purely by chance or if it reflects a genuine underlying effect. To make this distinction, we rely on methods that help us understand what the outcomes might look like if there were no actual difference between the conditions. This is where permutation tests come into play.

In a permutation test, we repeatedly “shuffle” or “permute” the group assignments in the data. Imagine taking each participant’s willingness to pay and randomly reassigning them to a condition over multiple iterations. After each reshuffling, we calculate the average willingness to pay in each condition based on the shuffled group assignments. This random reassignment assumes that the null hypothesis is true — that there’s no real difference between the conditions.

By calculating the differences in mean willingness to pay across these shuffled datasets, we build a null distribution. This null distribution represents the range of differences we might expect to see between experimental conditions if there were truly no effect of graph type viewed. We then compare our observed difference in willingness to pay from the actual data to this null distribution. If the observed difference is much larger or smaller than what we’d expect by chance, it suggests that the difference may reflect a true effect rather than random variation.

To see an example, let’s perform one shuffle.

Notice that the data frame now has the “real condition” (graph_type) and a randomly shuffled condition (shuffled_group).

Now, let’s recreate the earlier graph to examine willingness to pay across the conditions, but now use the shuffled groups rather than the real group/condition assignment.

This graph shows the average willingness to pay for the special boulder across randomly shuffled groups in the permutation, rather than the actual experimental conditions. By using these shuffled groups, we’re simulating what the differences between groups might look like if there were no true effect of the graph type viewed. This is a key idea in permutation testing: we create a distribution of differences under the assumption that group assignment is irrelevant to the outcome. Comparing our observed group differences to this distribution will help us determine whether the observed difference is likely due to chance or reflects a real effect.

We need many, many shuffled datasets for an accurate assessment.

When using permutation tests to test a hypothesis, we don’t rely on just a single shuffle of the data. Instead, we repeat the permutation process many times, just as we draw many bootstrap resamples in a bootstrap approach. Each time, we randomly shuffle the group assignments, calculate the average willingness to pay in each shuffled group, and compare the differences in willingness to pay across the shuffled groups. By doing this repeatedly, we generate a distribution of these means (and mean differences) under the assumption that there is no real effect of group assignment.

This distribution of permuted differences serves a similar purpose to the sampling distribution we generate with bootstrapping: it represents what we would expect to see by chance alone if the null hypothesis were true. In a permutation test, this distribution allows us to determine how unusual our observed difference is compared to what would happen randomly, helping us evaluate whether the observed difference is likely due to random variation or reflects a genuine effect.

Press Run Code on the code chunk below to perform the permutation process 1000 times, and then recreate the earlier graph using the mean and standard error for willingness to pay across the conditions averaged over the many shuffled datasets.

Using 1000 permutations, we calculate the mean and 95% confidence interval (CI) for each shuffled group. As expected, this yields virtually no difference in willingness to pay across groups. This outcome aligns with our expectation, as the shuffled groups have no true meaning.

Conduct a null hypothesis significance test using a permutation test

Let’s use the permutation test approach to determine if there is a significant difference in willingness to pay for the special boulder between two selected groups.

Step 1: Choose two conditions to compare

First, choose two conditions to compare. The code below will assign one condition to be called Group A, and the other condition to be called Group B. The code also creates a dummy-coded variable to compare Group B to Group A (which we’ll use later in the activity).

CI
CI rescaled
PI
HOPS

Press Run Code to create the subsetted data frame for the investigation.

Step 2: Compute descriptive statistics

What is the average willingness to pay for the special boulder in each of your selected conditions?

Press Run Code on the code chunk below to compute the mean and standard deviation of willingness to pay for the special boulder in your selected condition. The code also calculates the sample size of each group.

What is the mean difference in willingness to pay between the two groups?

Press Run Code to calculate the difference in willingness to pay between these two groups.

Last, let’s create a plot of the raw data. Press Run Code to visualize the distribution of willingness to pay for these two groups.

Step 3: State the null and alternative hypothesis

Null hypothesis: \(H_0: \mu_{\text{GroupA}} = \mu_{\text{GroupB}}\) (the two means are equal). Or equivalently: \(H_0: \mu_{\text{GroupA}} - \mu_{\text{GroupB}} = 0\) (the difference in means is zero)
Alternative hypothesis: \(H_a: \mu_{\text{GroupA}} \neq \mu_{\text{GroupB}}\) (the two means are not equal). Or equivalently: \(H_a: \mu_{\text{GroupA}} - \mu_{\text{GroupB}} \neq 0\) (the difference in means is not zero)

Step 4: Mimic the sampling distribution for the difference in group means under the null hypothesis

By using the permutations, we can approximate the sampling distribution of the difference in willingness to pay between the two groups under the null hypothesis. Press Run Code to generate this distribution by performing 1,000 permutations, calculating the mean willingness to pay for each shuffled group in each iteration. Then in the next step, we’ll compute the group differences.

Now, let’s compute the difference in mean willingness to pay between the groups for each permutation — we’ll call this new variable null_diff. Click Run Code to accomplish this task.

Now, we can visualize the expected difference in willingness to pay between the two groups under the null hypothesis.

If the null hypothesis is true, then we expect 95% of random samples selected to produce a mean difference in willingness to pay between the two dashed green lines. The pink line denotes the actual observed difference in willingness to pay between your two selected conditions.

How likely is the null hypothesis to be true given the actual observed difference?

Step 5: Query the permutations

In how many of the permuted samples is the calculated difference between groups as extreme (or more extreme) than our observed difference between groups?

Using the 1,000 shuffled data frames, we’ll identify permutations where the absolute difference between the means of the two shuffled groups is greater than or equal to the absolute difference between the observed means of the “real” groups (i.e., the two experimental conditions that you chose to study).

What does this mean intuitively?

Imagine the null hypothesis is true: there is no real difference in the average willingness to pay between the two groups we are comparing. Any difference in observed means is due purely to random chance or sampling error. The key question is, how unusual is our observed difference in means compared to what we would expect if there were no true difference?

By running 1,000 permutations, we simulate a world where the true difference in means is zero. For each permutation, we shuffle the group labels and calculate the difference in means between the two groups. This allows us to see the range of mean differences we might expect purely by chance when there is no real difference.

Since we’re not predicting which group should have a higher or lower mean (only that they should differ), we use the absolute value of the differences. This approach lets us measure both unusually high and unusually low values relative to the observed difference.

Here’s what we need to do to accomplish this task:

Label each permutation as “extreme” if its mean difference for the shuffled groups (in absolute terms) is at least as large as the observed difference between our “real” groups.
Count the “extreme” cases to estimate the likelihood of seeing a difference as extreme as ours by chance. If this likelihood is very small, it suggests that our observed difference in means is unlikely to have occurred by chance alone, providing evidence against the null hypothesis.

Press Run Code to tally the number of extreme samples.

What proportion of the permuted differences are as extreme as or more extreme than the observed difference?

Using the tally above, we can calculate the fraction of all permutations that yield a difference as large or larger than the one observed between our “real” groups. This fraction represents the probability of obtaining a sample with a difference in willingness to pay as extreme as the one observed, assuming the null hypothesis is true. This probability is known as the p-value.

If the p-value is very small, it suggests that such an extreme difference is unlikely to have occurred by chance alone, supporting the conclusion that there may be a true difference between the groups.

Step 6: Compute the standard deviation of the sampling distribution under the null

The standard error is the standard deviation of the sampling distribution, indicating how much variation we expect in the mean difference of willingness to pay between groups due to random sampling.

In our permutation test, the standard deviation of the differences in willingness to pay across the 1,000 shuffled datasets provides an estimate of this standard error under the null hypothesis. By calculating the spread of these permuted mean differences, we’re estimating the typical variation we would expect in the mean difference if there were no true difference between groups.

Press Run Code to compute the standard error.

Step 7: Calculate a test-statistic

How many standard errors (SE) away from the null is our observed difference (i.e., difference between the two groups in our observed sample)?

To determine how unusual our observed difference is compared to what we’d expect by chance, we need to see how far it is from the null hypothesis value, which we assume to be zero (i.e., no difference). In other words, we want to know: How many standard errors away from zero is our observed difference between the two “real” groups?

To calculate our t-statistic, we subtract the null hypothesis value (0) from the observed difference in willingness to pay between the two groups (\(\bar{x}_B - \bar{x}_A\)), then divide by the standard error. This t-statistic tells us how many standard errors away our observed difference is from the null hypothesis value.

The formula for the t-statistic is:

\[ t = \frac{(\bar{x}_B - \bar{x}_A) - 0}{SE} \]

Press Run Code on the code chunk below to compute the t-statistic.

We can visually represent our calculated test statistic overlaid onto the appropriate Student’s t-distribution. This will help us see where our observed t-statistic lies relative to the distribution we’d expect if the null hypothesis were true.

In order to compare two means, we must estimate two means (i.e., one for Group A, one for Group B) — thus, we lose two degrees of freedom (df). In other words, when estimating the difference between two means, the formula for calculating the df is n1 + n2 - 2, where n1 is the sample size for group 1 and n2 is the sample size for group 2. Once the df are computed, we can then compute the boundaries of the test statistic and create a graph of these boundaries and our observed t-statistic.

Press Run Code on the code chunk below to create a graph to depict the test statistic for comparing the means of these two groups.

On this graph, the dashed green lines indicate the critical boundaries, marking the middle 95% of the Student’s t-distribution for the given degrees of freedom (df). The pink line shows the calculated t-statistic for the difference in willingness to pay between the two selected conditions, measured in standard errors from the null hypothesis value (0 — i.e., no difference between groups).

If the pink line falls within the dashed green boundaries, we cannot reject the null hypothesis (we lack evidence that the group means differ).
If the pink line is outside the dashed green boundaries, we can reject the null hypothesis (indicating a significant difference between groups). In this example, such a result would suggest that the data visualization shown to participants affects their perceived willingness to pay.

Can the null hypothesis be rejected for the comparison of your selected conditions?

Step 8: Test the hypothesis with an independent samples t-test

To test whether there’s a meaningful difference in means between two groups, we have two primary approaches: a non-parametric approach (e.g., the permutation test we just worked through) and a parametric/theory-based approach.

A two-sample t-test is a parametric approach, meaning it relies on certain assumptions about the data:

Normality: The sampling distribution of the difference in means should be approximately normal. This assumption is generally met if each group’s data is roughly normal or if the sample sizes are large enough (thanks to the central limit theorem).
Equal Variance: The variability (spread) in each group should be approximately equal.

If these assumptions are reasonable for your data, an independent samples t-test can be a powerful tool. Here’s how the t-test works:

Calculate the Mean Difference: First, we calculate the difference in means between the two groups.
Estimate the Standard Error: Using the sample standard deviations and sizes of each group, we estimate the standard error, which tells us how much we’d expect the means to vary just by chance.
Compute the t-Statistic: The t-statistic measures how many standard errors the observed difference is from zero (our null hypothesis value, assuming no difference).

The formula for the t-statistic is:

\[ t = \frac{(\bar{x}_B - \bar{x}_A) - 0}{SE} \]

where:

\(\bar{x}_A\) and \(\bar{x}_B\) are the sample means for Groups A and B, respectively. The 0 subtracted in the numerator represents the null hypothesis value (i.e., no group difference).
\(SE\) is the standard error of the difference, calculated from the sample standard deviations and sample sizes of the groups. \(SE = \sqrt{\frac{s_A^2}{n_A} + \frac{s_B^2}{n_B}}\), where:\(s_A\) and \(s_B\) are the sample standard deviations for Groups A and B, \(n_A\) and \(n_B\) are the sample sizes for Groups A and B.

Press Run Code on the code chunk below to compute the test.

Notice the similarity between the t-statistic that we created using the permutations and the t-statistic in the t_test output (labeled statistic). Also, notice the similarity between the p-value that we created using the permutations and the p-value in the t_test output (labeled p_value).

Here’s a breakdown of the code for the t_test() function in this context:

wtp_final ~ group: This formula indicates that we are testing the difference in the mean values of willingness to pay between the groups defined by group.
var.equal = TRUE: This specifies that the variances of the two groups are assumed to be equal. If set to FALSE, the function would perform Welch’s t-test, which does not assume equal variances. We’ll discuss model assumptions in greater detail in Module 17.
order = c("B", "A"): This specifies the order in which the groups are subtracted. In this case, the mean of group A is subtracted from the mean of group B.
alternative = "two-sided": This specifies that the test is two-sided, meaning we are testing if there’s a significant difference in means, regardless of the direction (either group A is greater than group B or vice versa).

Step 9: Compute a 95% CI for the difference in willingness to pay

With the standard error estimated using our permutations, we can calculate the 95% CI for the observed difference between the two selected groups. Notice the similarity with the 95% CI in the t_test output.

Step 10: Test the hypothesis with a simple linear regression

We can equivalently specify the two sample t-test as a simple linear regression. Here, we regress willingness to pay on the dummy coded indicator designed to compare Group B to Group A.

Notice that the independent sample t-test and the simple linear regression produce IDENTICAL results for the difference in willingness to pay between the two groups. A two sample t-test and a simple linear regression in which the outcome is regressed on a grouping variable are equivalent models – you just get more information from using lm() to fit the model.